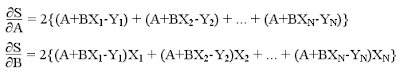El ajuste más sencillo de datos a fórmula que podamos llevar a cabo es aquél en el cual los datos manifiestan una tendencia linear, en la cual los datos parecen seguir una tendencia propia de una línea recta cuando son puestos en una gráfica. El primer paso, antes de que nada, consiste en plasmar en una gráfica los datos de los que disponemos para saber si en efecto existe alguna tendencia (ya sea linear o no linear) de los datos para agruparse siguiendo cierta tendencia, detrás de la cual posiblemente exista alguna relación natural que eventualmente pueda ser expresada con una fórmula sencilla. Si la gráfica de los datos de varios pares de mediciones de dos cantidades variables, una de las cuales tal vez pueda ser variada a voluntad, resulta ser una como la siguiente:
podemos ver que no parece haber ninguna correlación entre los datos graficados. Sin embargo, si la gráfica resulta ser una como la siguiente:
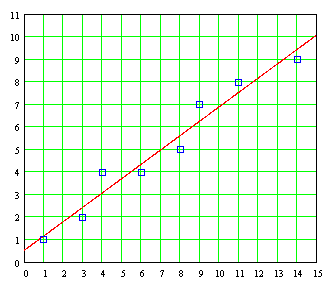
entonces esto ya manifiesta cierta tendencia. Estos datos, supuestamente obtenidos por la vía experimental, casi siempre adolecerán de un error aleatorio (ocurriendo al azar) que denotaremos con la letra griega ε (equivalente a la letra latina "e"). Si no fuese por este error, posiblemente los datos caerían todos en una línea recta o en una curva suave y continua propia del fenómeno que está siendo descrito por los datos. En la última gráfica, resulta tentador trazar "a mano" sobre la misma una línea recta que esté lo más cerca posible de todos los datos, una línea recta como la siguiente:

El problema con un trazado "a mano" de la línea recta es que distintas personas obtendrán distintas líneas según sus propios criterios subjetivos, y posiblemente nadie tendrá la misma recta, no habiendo forma alguna de saber cuál de todas ellas sea la mejor. Es por ello que, con el fin de unificar criterios y obtener una misma respuesta en todos los casos, necesitamos recurrir a un criterio matemático. Este criterio nos lo dá el método de los mínimos cuadrados, desarrollado por el "príncipe de las matemáticas" Carl Friedrich Gauss.
La idea detrás del método de los mínimos cuadrados es la siguiente: si sobre un conjunto de datos en una gráfica que parecen agruparse siguiendo una tendencia marcada por una línea recta se traza una línea recta, entonces de todas las líneas distintas que puedan trazarse podemos tratar de encontrar aquella que produzca "el mejor ajuste" (en inglés esto se llama best fit) de acuerdo a algún criterio matemático. Esta línea pueda ser aquella tal que la "distancia promedio" de todos los puntos en la gráfica hacia esa línea ideal sea la menor distancia promedio posible. Aunque las distancias de cada punto hacia la línea ideal se pueden definir de modo tal que sean perpendiculares a dicha línea, como lo muestra el siguiente dibujo derecho:
la manipulación matemática del problema se puede simplificar mucho si en vez de utilizar tales distancias perpendiculares a la línea ideal utilizamos las distancias verticales según el eje vertical de la gráfica como lo muestra el dibujo izquierdo de arriba.
Aunque podríamos tratar de utilizar los valores absolutos │di│de las distancias de cada uno de los puntos i hacia la línea ideal (los valores absolutos eliminan la presencia de valores negativos que promediados con los valores positivos terminarían "cancelando" nuestra intención de obtener un promedio útil), el problema principal es que el valor absoluto de cualquier variable no puede ser diferenciado matemáticamente de una manera convencional, no se presta fácilmente a una derivación matemática mediante los recursos usuales del cálculo diferencial, lo cual es un inconveniente cuando se van a utilizar las herramientas del cálculo para la obtención de máximos y mínimos. Es por ello que utilizamos la suma de los cuadrados de las distancias en lugar de los valores absolutos de las mismas, ya que esto permite tratar a dichas valores, conocidos como residuales, como una cantidad continuamente diferenciable. Sin embargo, esta técnica tiene la desventaja de que al utilizarse los cuadrados de las distancias aquellos puntos aislados que estén muy alejados de la línea ideal tendrán un efecto sobre el ajuste, algo que no hay que perder de vista cuando aparezcan datos aislados en la gráfica que parezcan demasiado alejados de la línea ideal y que posiblemente sean indicativos de un yerro de medición o de un dato mal registrado.
Para una serie de datos que parecen mostrar una tendencia linear, de acuerdo con el método de los mínimos cuadrados se supone desde el principio la existencia de una línea "ideal" que proporciona el "mejor ajuste" (best fit) conocido como "ajuste de mínimos cuadrados" (least squares fit). La ecuación de esta "recta ideal" será:
en donde A y B son los parámetros (constantes numéricas) que serán determinados bajo el criterio de los mínimos cuadrados.
Dada una cantidad N de pares de puntos experimentales (X1,Y1), (X2,Y2), (X3,Y3), etc., entonces para cada punto experimental correspondiendo a cada valor de la variable independiente X=X1,X2,X3,...,XN habrá un valor calculado yi= y1,y2,y3,... usando la recta "ideal", el cual será:
La diferencia entre cada valor real de Y=Y1,Y2,Y3,...,YN y cada valor calculado para su correspondiente Xi usando la recta ideal nos dá la "distancia" vertical Di que aleja a ambos valores:
Cada una de estas distancias Di es conocida dentro de las matemáticas estadísticas como el residual.
Para encontrar la recta "ideal", usaremos los procedimientos del cálculo diferencial establecidos para la determinación de máximos y mínimos. Un primer intento nos llevaría a intentar encontrar la recta que minimice la suma de las distancias
Sin embargo, este esquema no nos servirá de mucho, debido a que al efectuar los cálculos para determinar el valor de cada distancia Di algunos puntos "reales" quedarán encima de la recta y otros quedarán debajo de la misma, con lo cual algunas de las distancias serán positivas y otras negativas (quizá repartidas en partes iguales) cancelándose de este modo en gran parte sus contribuciones a la construcción de la función que queremos minimizar. Esto nos conduce de inmediato a intentar utilizar los valores absolutos de las distancias:
Pero este esquema presenta otra dificultad. Cualquier función matemática definida en términos del valor absoluto no es una función continua y por lo tanto continuamente diferenciable. Tratar de maximizar o minimizar una función así nos presenta más problemas que los que nos resuelve. Esto nos lleva a intentar otro esquema en el cual también sumamos las distancias Di pero sin el problema de la cancelación mutua de términos por haber términos positivos como negativos. La estrategia consiste en utilizar los cuadrados de las distancias:
Con esta definición, la expresión general que deseamos minimizar está dada por:
Las incógnitas de la recta ideal que estamos buscando son los parámetros A y B. Con respecto a estas dos incógnitas es como tenemos que llevar a cabo la minimización de S. Si fuese un solo parámetro, una diferenciación ordinaria bastaría. Pero como se trata de dos parámetros, tenemos que llevar a cabo dos diferenciaciones separadas usando derivadas parciales en las cuales diferenciamos con respecto a un parámetro manteniendo al otro constante.
Del cálculo, S será un mínimo cuando las derivadas parciales con respecto a A y B sean cero. Estas derivadas parciales son las siguientes:
La solución de estas ecuaciones nos dá las ecuaciones requeridas:
en donde estamos utilizando la siguiente simplificación simbólica de la notación:
Las dos ecuaciones las podemos reacomodar de la siguiente manera:
teniendo con esto dos ecuaciones lineares que se pueden resolver como ecuaciones simultáneas ya sea directamente o mediante el método de Cramer (determinantes), obteniendo así las siguientes fórmulas:
De este modo, la substitución de datos en las dos fórmulas nos proporciona los valores de los parámetros A y B que estamos buscando para obtener así la "recta ideal", la recta que nos proporciona el mejor ajuste posible de todas las que podamos trazar bajo los criterios que hemos definido. Puesto que estamos minimizando una función que minimiza la suma de los cuadrados de las distancias (residuales), este método como ya se mencionó es conocido universalmente como el método de los mínimos cuadrados.
PROBLEMA: Dados los siguientes valores, obtener la recta de los mínimos cuadrados:
Para usar las ecuaciones requeridas para obtener la recta de los mínimos cuadrados, resulta conveniente acomodar las sumaciones en una tabla como la que se muestra a continuación:
De esta tabla de resultados intermedios obtenemos:
Y usando las fórmulas arriba obtenidas:
La recta de mínimos cuadrados es entonces:
La gráfica de esta línea recta superimpuesta sobre los pares de puntos individuales es la siguiente:
Podemos ver que el ajuste es razonablemente bueno. Y, lo más importante, distintos investigadores obtendrán exactamente el mismo resultado bajo el criterio de los míminos cuadrados para este tipo de problemas. Cabe resaltar que la mecanización de la evaluación de estos datos mediante arreglos de columnas como las que fueron utilizadas arriba obteniendo ΣX, ΣY, ΣX² y ΣXY puede llevarse a cabo en una "hoja de trabajo" como EXCEL.
Para un conjunto numeroso de pares de datos, en otros tiempos estos cálculos solían resultar tediosos y sujetos a equivocaciones. Afortunadamente, con el advenimiento de las calculadoras programables de bolsillo así como programas computacionales que hoy en día pueden realizar en una computadora de escritorio cálculos aritméticos para los cuales hace apenas unas dos décadas requerían computadoras costosas y programas sofisticados en algún lenguaje de programación científica como FORTRAN, estos cálculos se pueden mecanizar a grado tal que en vez de tener que utilizarse cantidades desmedidas de tiempo en la realización de los cálculos el énfasis hoy en día está en el análisis y la interpretación de los resultados.
Cuando sobre una base de datos obtenidos experimentalmente o datos obtenidos de una muestra tomada entre una población queremos estimar el valor de una variable Y que corresponda a cierto valor de otra variable X a partir de la curva de mínimos cuadrados que mejor se ajuste a los datos, se acostumbra llamar a la curva resultante la curva de regresión de Y en X, puesto que Y es estimada de X. Si la curva es una línea recta, entonces llamamos a esa línea la línea de regresión de Y en X. Un análisis llevado a cabo mediante el método de los mínimos cuadrados es llamado también análisis de regresión, y los programas computacionales que pueden efectuar cálculos de mínimos cuadrados son llamados programas de regresión.
Si, por el contrario, en lugar de estimar el valor de Y a partir del valor de X lo que deseamos es estimar el valor de X a partir de Y, entonces usaríamos una curva de regresión de X en Y, lo cual implica simplemente intercambiar las variables en el diagrama (y en las ecuaciones normales) de tal manera que X sea la variable dependiente y Y la variable independiente, lo cual a su vez significa reemplazar las distancias verticales D usadas en la derivación de la recta de mínimos cuadrados por distancias horizontales:
Un detalle interesante es que, por lo general, para un conjunto dado de datos la línea de regresión de Y en X y la línea de regresión de X en Y son dos líneas diferentes que no coinciden exactamente en un diagrama, aunque de cualquier modo están tan cercanas la una de la otra que se podrían confundir.
PROBLEMA: Dado el siguiente conjunto de datos:
a) Obtener la línea de regresión de Y en X, considerando a Y como variable dependiente y a X como variable independiente.
b) Obtener la línea de regresión de X en Y, considerando a X como variable dependiente y a Y como variable independiente.
a) Considerando a Y como la variable dependiente y a X como la variable independiente, la ecuación de la línea de mínimos cuadrados es Y=A+BX, y las ecuaciones normales son:
Llevando a cabo las sumaciones, las ecuaciones normales se convierten en:
Simultaneando ambas ecuaciones, obtenemos A=6/11 y B=7/11. Entonces la línea de mínimos cuadrados es:
b) Considerando a X como la variable dependiente y a Y como la variable independiente, la ecuación de mínimos cuadrados es ahora X=P+QY, y las ecuaciones normales serán:
Llevando a cabo las sumaciones, las ecuaciones normales se convierten en:
Simultaneando ambas ecuaciones, obtenemos P=-1/2 y Q=3/2. Entonces la línea de mínimos cuadrados es:
Para fines comparativos, podemos despejar esta última fórmula para poner a Y en función de X, obteniendo:
Notamos que las líneas de regresión obtenidas en (a) y en (b) son diferentes. A continuación tenemos una gráfica que muestra a ambas líneas:
Un parámetro importante para medir qué tan bien es el "ajuste" de varios datos experimentales a una línea recta obtenida de los mínimos por el método de los mínimos cuadrados es el coeficiente de correlación. Cuando todos los datos quedan situados exactamente sobre una línea recta, entonces el coeficiente de correlación es la unidad, y conforme los datos en una gráfica se van mostrando cada vez más dispersos en relación a la recta entonces el coeficiente de correlación va disminuyendo gradualmente como lo muestran los ejemplos siguientes:
Como una cortesía del Profesor Victor Miguel Ponce, catedrático e investigador en San Diego State University, se encuentran disponibles al público en su página personal en Internet varios programas para mecanizar los cálculos requeridos para "ajustar" conjunto de datos con tendencia linear a una línea de "mínimos cuadrados". La página que proporciona todos los programas es:
http://ponce.sdsu.edu/online_calc.php
bajo el encabezado de "Regression". La página que nos interesa para obtener un ajuste de datos a una línea recta se encuentra en la dirección:
http://ponce.sdsu.edu/onlineregression11.php
Para utilizar el programa citado, introducimos primero el tamaño del arreglo (array), o sea la cantidad de pares de datos, tras lo cual introducimos los valores apareados de datos en forma ordenada empezando primero con los valores de y separados por comas, seguido por los valores de x, también separados por comas. Hecho esto, oprimimos "Calculate" en el extremo inferior de la página, con lo cual obtenemos los valores α y ß para la línea de mínimos cuadrados y=α+ßx, el coeficiente de correlación r, el error estandard de la estimación, así como las dispersiones (desviaciones estándard) σx y σy de los datos xi y de los datos yi.
Como un ejemplo del uso de este programa, obtengamos la línea de mínimos cuadrados para los siguientes pares de datos:
De acuerdo con este programa, la línea de mínimos cuadrados es:
Y el coeficiente de correlación es r=1.0, mientras que el error estándard de la estimación es cero, lo cual como veremos posteriormente nos dice que todos los pares de datos forman parte de la línea de mínimos cuadrados. Si graficamos la línea de mínimos cuadrados y graficamos sobre ella los pares de datos (xi,yi), comprobaremos que efectivamente todos los datos están alineados directamente sobre una recta:
lo cual nos confirma que el criterio matemático que estamos utilizando para obtener la línea de los mínimos cuadrados, la definición que tenemos del índice de correlación r son correctos, y la definición que tenemos del error estándard de la estimación, son correctos.
Hasta aquí hemos considerado un "ajuste de mínimos cuadrados" relacionados con una línea que pudiéramos llamar "ideal" desde el punto de vista matemático, en donde tenemos una variable independiente (causa) que produce una influencia sobre alguna variable dependiente (efecto). Pero se puede dar el caso de que tengamos una situación en la cual los valores que tome cierta variable dependiente se deban no a uno sino a dos o más factores. En tal caso, si la dependencia individual a causa de cada uno de los factores -manteniendo los demás constantes- es una dependencia linear, podemos extender el método de los mínimos cuadrados para cubrir esta situación, tal y como lo hicimos cuando había una sola variable independiente. Esto es conocido como una regresión linear múltiple. Para dos variables X1 y X2, esta dependencia la representamos como Y=f(X1,X2). Si tenemos un conjunto de datos experimentales para una situación como esta, la grafica de los datos se tiene que llevar a cabo en tres dimensiones, y presenta un aspecto como el siguiente:
En esta gráfica, la altura de cada punto representa el valor de Y para cada cada par de valores X1 y X2. Representando los puntos sin mostrar explícitamente las "alturas" de los puntos hacia el plano horizontal Y=0, la gráfica tridimensional toma el siguiente aspecto:
El método de los mínimos cuadrados utilizado para ajustar un conjunto de datos a una recta de mínimos cuadrados también se puede extender para obtener una fórmula de mínimos cuadrados, en cuyo caso para dos variables la ecuación de regresión será la siguiente:
Erróneamente y frecuentemente, esta ecuación es tomada como representando una línea. Sin embargo, no es una línea, es una superficie. Si llevamos a cabo un ajuste de mínimos cuadrados sobre esta fórmula linear con dos factores X1 y X2, obtenemos lo que se conoce como una superficie de regresión, que en este caso es una superficie plana:
Para los datos mostrados arriba, esta superficie de regresión tiene un aspecto como el que se muestra a continuación:
Si queremos obtener las ecuaciones para este plano de mínimos cuadrados, procedemos exactamente de la misma manera como lo hicimos para obtener las fórmulas con las cuales evaluamos los parámetros para obtener la recta de mínimos cuadrados; esto es, definimos las distancias verticales de cada uno de los pares ordenados de puntos hacia este plano de mínimos cuadrados:
Por extensión, los problemas que involucran más de las dos variables X y Y se tratan de una manera análoga a como lo hicimos con dos parámetros. Para obtener las ecuaciones de regresión para dos variables independientes X1 y X2, supóngase que empezamos con una relación entre las tres variables que puede ser descrita mediante la siguiente fórmula:
la cual es una fórmula linear en las variables Y, X1 y X2. Tenemos aquí tres parámetros independientes α, ß1 y ß2. Los valores de Y en esta línea que corresponden a X1=X11,X12,X13, ... ,X1N y X2=X21,X22,X23, ... ,X2N (usamos aquí el subscripto para distinguir cada una de las dos variables X1 y X2, y el superscripto para llevar a cabo eventualmente las sumaciones sobre los valores que hay de cada una de dichas variables) son α+ß1X11+ß2X21, α+ß1X12+ß2X22, α+ß1X13+ß2X23, ... , α+ß1X1N+ß2X2N, mientras que los valores actuales son Y1, Y2, Y3, ... ,YN respectivamente. Entonces, al igual que como lo hicimos con la ecuación de regresión en función de una sola variable, definimos las "distancias" producidas por cada trío de datos experimentales a los valores Yi de modo tal que la suma de los cuadrados de dichas distancias sea:
Del cálculo, S será un mínimo cuando las derivadas parciales de S con respecto a los parámetros α, ß1 y ß2 sean iguales a cero:
Procediendo como lo hicimos cuando teníamos dos parámetros en lugar de tres, esto nos produce el siguiente conjunto de ecuaciones:
Estas son las ecuaciones normales requeridas para poder obtener la regresión de Y en X1 y X2. Al efectuar los cálculos, nos resultan tres ecuaciones simultáneas de las cuales se obtienen los parámetros α, ß1 y ß2.
Existe una razón por la cual estas ecuaciones son llamadas ecuaciones normales. Si representamos al conjunto de datos correspondiente a la variable X1 como un vector X1 y al conjunto de datos correspondiente a la variable X2 como otro vector X2, considerando que estos vectores son independientes el uno del otro (usando un término del álgebra linear, linearmente independientes, lo cual significa que no son un simple múltiplo el uno del otro apuntando físicamente en la misma dirección), entonces podemos situar a dichos vectores en un plano. Por otro lado, podemos considerar a la suma de los cuadrados de las diferencias Di usadas en la derivación de las ecuaciones normales también como la magnitud de un vector Di, recordando que la longitud cuadrada de un vector es igual a la suma de los cuadrados de sus elementos (teorema de Pitágoras extendido a n dimensiones). Esto hace que el principio del "mejor ajuste" sea equivalente a buscar aquél vector diferencia Di que corresponda a la menor distancia posible hacia el plano formado por los vectores X1 y X2. Y esa menor distancia posible es un vector perpendicular o vector normal:
al plano definido por los vectores X1 y X2 (o mejor dicho, al plano formado por la combinación linear de los vectores ß1X1+ß2X2).
Aunque podemos repetir aquí las fórmulas que corresponderán al caso de dos variables X1 y X2, habiendo entendido lo que es un "plano de míminos cuadrados" podemos recurrir a uno de muchos programas computacionales disponibles comercialmente o a través de Internet. La página personal del Profesor Victor Miguel Ponce citada arriba nos ofrece los medios para poder llevar a cabo un "ajuste de mínimos cuadrados" cuando se trata del caso de de dos variables X1 y X2, accesible en la siguiente dirección:
http://ponce.sdsu.edu/onlineregression13.php
PROBLEMA: Obtener la fórmula del plano que mejor se ajusta a la representación del siguiente conjunto de datos:
Estos datos, representados en tres dimensiones, muestran el siguiente aspecto:
Para este conjunto de datos, la fórmula que corresponde a la superficie de regresión es la siguiente:
A continuación tenemos un gráfico animado de la regresión linear múltiple en X1 y X2 representada por la fórmula:
en el cual X1 y X2 son variados desde -10 hasta +10 y la gráfica tridimensional es rotada girándola alrededor del eje Y, razón por la cual este tipo de gráficas son conocidas con el nombre de "spin plot" (es necesario ampliar la imagen para poder ver la acción animada):
El modelaje que hemos llevado a cabo se puede extender a tres variables, a cuatro variables, etc., y podemos obtener una ecuación de regresión linear múltiple:
Desafortunadamente, para más de dos variables ya no es posible hacer un graficado multi-dimensional, y en vez de confiar en nuestra intuición geométrica tenemos que confiar en nuestra intuición matemática. Después de cierta práctica, podemos abandonar nuestra dependencia en representaciones gráficas extendiendo lo que aprendimos hacia un mundo multi-dimensional aunque no nos sea posible poder visualizar lo que está ocurriendo, dando el paso crucial de generalización o abstracción que nos permite prescindir de los detalles particulares y aún así poder continuar trabajando como si nada hubiera pasado.
Una cosa importante que no hemos mencionado aún es que, para el caso de dos variables (así como más de tres variables), no hemos tomado en cuenta los posibles efectos de interacción que pueda haber entre las variables independientes. Estos efectos de interacción, que se dan con cierta frecuencia en el campo de las aplicaciones prácticas, se pueden modelar en su caso más sencillo con una fórmula como la siguiente:
Cuando no hay interacción alguna entre las variables , el parámetro ß12 mostrado en esta fórmula es cero. Pero si hay algún tipo de interacción, dependiendo de la magnitud del parámetro ß12 con respecto a los demás parámetros ß0, ß1 y ß2 esta interacción podría ser de tal magnitud que inclusive podría nulificar la importancia de los términos variables ß1X1 y ß2X2. Este tema por sí solo es lo suficientemente amplio como para requerir ser tratado por separado en otra sección de esta obra.
La idea detrás del método de los mínimos cuadrados es la siguiente: si sobre un conjunto de datos en una gráfica que parecen agruparse siguiendo una tendencia marcada por una línea recta se traza una línea recta, entonces de todas las líneas distintas que puedan trazarse podemos tratar de encontrar aquella que produzca "el mejor ajuste" (en inglés esto se llama best fit) de acuerdo a algún criterio matemático. Esta línea pueda ser aquella tal que la "distancia promedio" de todos los puntos en la gráfica hacia esa línea ideal sea la menor distancia promedio posible. Aunque las distancias de cada punto hacia la línea ideal se pueden definir de modo tal que sean perpendiculares a dicha línea, como lo muestra el siguiente dibujo derecho:
la manipulación matemática del problema se puede simplificar mucho si en vez de utilizar tales distancias perpendiculares a la línea ideal utilizamos las distancias verticales según el eje vertical de la gráfica como lo muestra el dibujo izquierdo de arriba.
Aunque podríamos tratar de utilizar los valores absolutos │di│de las distancias de cada uno de los puntos i hacia la línea ideal (los valores absolutos eliminan la presencia de valores negativos que promediados con los valores positivos terminarían "cancelando" nuestra intención de obtener un promedio útil), el problema principal es que el valor absoluto de cualquier variable no puede ser diferenciado matemáticamente de una manera convencional, no se presta fácilmente a una derivación matemática mediante los recursos usuales del cálculo diferencial, lo cual es un inconveniente cuando se van a utilizar las herramientas del cálculo para la obtención de máximos y mínimos. Es por ello que utilizamos la suma de los cuadrados de las distancias en lugar de los valores absolutos de las mismas, ya que esto permite tratar a dichas valores, conocidos como residuales, como una cantidad continuamente diferenciable. Sin embargo, esta técnica tiene la desventaja de que al utilizarse los cuadrados de las distancias aquellos puntos aislados que estén muy alejados de la línea ideal tendrán un efecto sobre el ajuste, algo que no hay que perder de vista cuando aparezcan datos aislados en la gráfica que parezcan demasiado alejados de la línea ideal y que posiblemente sean indicativos de un yerro de medición o de un dato mal registrado.
Para una serie de datos que parecen mostrar una tendencia linear, de acuerdo con el método de los mínimos cuadrados se supone desde el principio la existencia de una línea "ideal" que proporciona el "mejor ajuste" (best fit) conocido como "ajuste de mínimos cuadrados" (least squares fit). La ecuación de esta "recta ideal" será:
Y = A + BX
en donde A y B son los parámetros (constantes numéricas) que serán determinados bajo el criterio de los mínimos cuadrados.
Dada una cantidad N de pares de puntos experimentales (X1,Y1), (X2,Y2), (X3,Y3), etc., entonces para cada punto experimental correspondiendo a cada valor de la variable independiente X=X1,X2,X3,...,XN habrá un valor calculado yi= y1,y2,y3,... usando la recta "ideal", el cual será:
y1 = A + BX1
y2 = A + BX2
y3 = A + BX3
.
.
.
yN = A + BXN
y2 = A + BX2
y3 = A + BX3
.
.
.
yN = A + BXN
La diferencia entre cada valor real de Y=Y1,Y2,Y3,...,YN y cada valor calculado para su correspondiente Xi usando la recta ideal nos dá la "distancia" vertical Di que aleja a ambos valores:
D1 = A + BX1 - Y1
D2 = A + BX2 - Y2
D3 = A + BX3 - Y3
.
.
.
DN = A + BXN - YN
D2 = A + BX2 - Y2
D3 = A + BX3 - Y3
.
.
.
DN = A + BXN - YN
Cada una de estas distancias Di es conocida dentro de las matemáticas estadísticas como el residual.
Para encontrar la recta "ideal", usaremos los procedimientos del cálculo diferencial establecidos para la determinación de máximos y mínimos. Un primer intento nos llevaría a intentar encontrar la recta que minimice la suma de las distancias
S = D1 + D2 + D3 + ... + DN
Sin embargo, este esquema no nos servirá de mucho, debido a que al efectuar los cálculos para determinar el valor de cada distancia Di algunos puntos "reales" quedarán encima de la recta y otros quedarán debajo de la misma, con lo cual algunas de las distancias serán positivas y otras negativas (quizá repartidas en partes iguales) cancelándose de este modo en gran parte sus contribuciones a la construcción de la función que queremos minimizar. Esto nos conduce de inmediato a intentar utilizar los valores absolutos de las distancias:
S = |D1| + |D2| + |D3| + ... + |DN|
Pero este esquema presenta otra dificultad. Cualquier función matemática definida en términos del valor absoluto no es una función continua y por lo tanto continuamente diferenciable. Tratar de maximizar o minimizar una función así nos presenta más problemas que los que nos resuelve. Esto nos lleva a intentar otro esquema en el cual también sumamos las distancias Di pero sin el problema de la cancelación mutua de términos por haber términos positivos como negativos. La estrategia consiste en utilizar los cuadrados de las distancias:
S = D1² + D2² + D3² + ... + DN²
Con esta definición, la expresión general que deseamos minimizar está dada por:
S = (A+BX1-Y1)² + (A+BX2-Y2)² + (A+BX3-Y3)² + ... + (A+BXN-YN)²
Las incógnitas de la recta ideal que estamos buscando son los parámetros A y B. Con respecto a estas dos incógnitas es como tenemos que llevar a cabo la minimización de S. Si fuese un solo parámetro, una diferenciación ordinaria bastaría. Pero como se trata de dos parámetros, tenemos que llevar a cabo dos diferenciaciones separadas usando derivadas parciales en las cuales diferenciamos con respecto a un parámetro manteniendo al otro constante.
Del cálculo, S será un mínimo cuando las derivadas parciales con respecto a A y B sean cero. Estas derivadas parciales son las siguientes:
La solución de estas ecuaciones nos dá las ecuaciones requeridas:
AN + B Σ X - ΣY = 0
AΣX + BΣX² - ΣXY = 0
en donde estamos utilizando la siguiente simplificación simbólica de la notación:
Las dos ecuaciones las podemos reacomodar de la siguiente manera:
AN + BΣX = ΣY
AΣX + BΣX² = ΣXY
teniendo con esto dos ecuaciones lineares que se pueden resolver como ecuaciones simultáneas ya sea directamente o mediante el método de Cramer (determinantes), obteniendo así las siguientes fórmulas:
De este modo, la substitución de datos en las dos fórmulas nos proporciona los valores de los parámetros A y B que estamos buscando para obtener así la "recta ideal", la recta que nos proporciona el mejor ajuste posible de todas las que podamos trazar bajo los criterios que hemos definido. Puesto que estamos minimizando una función que minimiza la suma de los cuadrados de las distancias (residuales), este método como ya se mencionó es conocido universalmente como el método de los mínimos cuadrados.
PROBLEMA: Dados los siguientes valores, obtener la recta de los mínimos cuadrados:
Para usar las ecuaciones requeridas para obtener la recta de los mínimos cuadrados, resulta conveniente acomodar las sumaciones en una tabla como la que se muestra a continuación:
De esta tabla de resultados intermedios obtenemos:
(ΣY)(ΣX²) - (ΣX)(ΣXY) = (40)(524) - (56)(364) = 6
NΣXY - (ΣX)(ΣY) = (8)(364) - (56)(40) = 7
NΣX² - (ΣX)² = (8)(524) - (56)² = 11
NΣXY - (ΣX)(ΣY) = (8)(364) - (56)(40) = 7
NΣX² - (ΣX)² = (8)(524) - (56)² = 11
Y usando las fórmulas arriba obtenidas:
A = [(ΣY)(ΣX²) - (ΣX)(ΣXY)]/[NΣX² - (ΣX)²] = 6/11
A = .545
A = .545
B = [NΣXY - (ΣX)(ΣY)]/[NΣX² - (ΣX)²] = 7/11
B = .636
B = .636
La recta de mínimos cuadrados es entonces:
Y = A + BX
Y = .545 + .636X
Y = .545 + .636X
La gráfica de esta línea recta superimpuesta sobre los pares de puntos individuales es la siguiente:
Podemos ver que el ajuste es razonablemente bueno. Y, lo más importante, distintos investigadores obtendrán exactamente el mismo resultado bajo el criterio de los míminos cuadrados para este tipo de problemas. Cabe resaltar que la mecanización de la evaluación de estos datos mediante arreglos de columnas como las que fueron utilizadas arriba obteniendo ΣX, ΣY, ΣX² y ΣXY puede llevarse a cabo en una "hoja de trabajo" como EXCEL.
Para un conjunto numeroso de pares de datos, en otros tiempos estos cálculos solían resultar tediosos y sujetos a equivocaciones. Afortunadamente, con el advenimiento de las calculadoras programables de bolsillo así como programas computacionales que hoy en día pueden realizar en una computadora de escritorio cálculos aritméticos para los cuales hace apenas unas dos décadas requerían computadoras costosas y programas sofisticados en algún lenguaje de programación científica como FORTRAN, estos cálculos se pueden mecanizar a grado tal que en vez de tener que utilizarse cantidades desmedidas de tiempo en la realización de los cálculos el énfasis hoy en día está en el análisis y la interpretación de los resultados.
Cuando sobre una base de datos obtenidos experimentalmente o datos obtenidos de una muestra tomada entre una población queremos estimar el valor de una variable Y que corresponda a cierto valor de otra variable X a partir de la curva de mínimos cuadrados que mejor se ajuste a los datos, se acostumbra llamar a la curva resultante la curva de regresión de Y en X, puesto que Y es estimada de X. Si la curva es una línea recta, entonces llamamos a esa línea la línea de regresión de Y en X. Un análisis llevado a cabo mediante el método de los mínimos cuadrados es llamado también análisis de regresión, y los programas computacionales que pueden efectuar cálculos de mínimos cuadrados son llamados programas de regresión.
Si, por el contrario, en lugar de estimar el valor de Y a partir del valor de X lo que deseamos es estimar el valor de X a partir de Y, entonces usaríamos una curva de regresión de X en Y, lo cual implica simplemente intercambiar las variables en el diagrama (y en las ecuaciones normales) de tal manera que X sea la variable dependiente y Y la variable independiente, lo cual a su vez significa reemplazar las distancias verticales D usadas en la derivación de la recta de mínimos cuadrados por distancias horizontales:
Un detalle interesante es que, por lo general, para un conjunto dado de datos la línea de regresión de Y en X y la línea de regresión de X en Y son dos líneas diferentes que no coinciden exactamente en un diagrama, aunque de cualquier modo están tan cercanas la una de la otra que se podrían confundir.
PROBLEMA: Dado el siguiente conjunto de datos:
a) Obtener la línea de regresión de Y en X, considerando a Y como variable dependiente y a X como variable independiente.
b) Obtener la línea de regresión de X en Y, considerando a X como variable dependiente y a Y como variable independiente.
a) Considerando a Y como la variable dependiente y a X como la variable independiente, la ecuación de la línea de mínimos cuadrados es Y=A+BX, y las ecuaciones normales son:
ΣY = AN + BΣX
ΣXY = AΣX + BΣX²
ΣXY = AΣX + BΣX²
Llevando a cabo las sumaciones, las ecuaciones normales se convierten en:
8A + 56B = 40
56A + 524B = 364
56A + 524B = 364
Simultaneando ambas ecuaciones, obtenemos A=6/11 y B=7/11. Entonces la línea de mínimos cuadrados es:
Y = 6/11 + (7/11)X
Y = .545 + .636X
Y = .545 + .636X
b) Considerando a X como la variable dependiente y a Y como la variable independiente, la ecuación de mínimos cuadrados es ahora X=P+QY, y las ecuaciones normales serán:
ΣX = PN + QΣY
ΣXY = PΣY + QΣY²
ΣXY = PΣY + QΣY²
Llevando a cabo las sumaciones, las ecuaciones normales se convierten en:
8P + 40Q = 56
40P + 256Q = 364
40P + 256Q = 364
Simultaneando ambas ecuaciones, obtenemos P=-1/2 y Q=3/2. Entonces la línea de mínimos cuadrados es:
X = -1/2 + (3/2)Y
X = -0.5 + 1.5Y
X = -0.5 + 1.5Y
Para fines comparativos, podemos despejar esta última fórmula para poner a Y en función de X, obteniendo:
Y = .333 + .667X
Notamos que las líneas de regresión obtenidas en (a) y en (b) son diferentes. A continuación tenemos una gráfica que muestra a ambas líneas:
Un parámetro importante para medir qué tan bien es el "ajuste" de varios datos experimentales a una línea recta obtenida de los mínimos por el método de los mínimos cuadrados es el coeficiente de correlación. Cuando todos los datos quedan situados exactamente sobre una línea recta, entonces el coeficiente de correlación es la unidad, y conforme los datos en una gráfica se van mostrando cada vez más dispersos en relación a la recta entonces el coeficiente de correlación va disminuyendo gradualmente como lo muestran los ejemplos siguientes:
Como una cortesía del Profesor Victor Miguel Ponce, catedrático e investigador en San Diego State University, se encuentran disponibles al público en su página personal en Internet varios programas para mecanizar los cálculos requeridos para "ajustar" conjunto de datos con tendencia linear a una línea de "mínimos cuadrados". La página que proporciona todos los programas es:
http://ponce.sdsu.edu/online_calc.php
bajo el encabezado de "Regression". La página que nos interesa para obtener un ajuste de datos a una línea recta se encuentra en la dirección:
http://ponce.sdsu.edu/onlineregression11.php
Para utilizar el programa citado, introducimos primero el tamaño del arreglo (array), o sea la cantidad de pares de datos, tras lo cual introducimos los valores apareados de datos en forma ordenada empezando primero con los valores de y separados por comas, seguido por los valores de x, también separados por comas. Hecho esto, oprimimos "Calculate" en el extremo inferior de la página, con lo cual obtenemos los valores α y ß para la línea de mínimos cuadrados y=α+ßx, el coeficiente de correlación r, el error estandard de la estimación, así como las dispersiones (desviaciones estándard) σx y σy de los datos xi y de los datos yi.
Como un ejemplo del uso de este programa, obtengamos la línea de mínimos cuadrados para los siguientes pares de datos:
x(1) = 1, y(1) = 5
x(2) = 2, y(2) =7
x(3) = 4, y(3) = 11
x(4) = 5, y(4) = 13
x(5) = 9, y(5) = 21
x(2) = 2, y(2) =7
x(3) = 4, y(3) = 11
x(4) = 5, y(4) = 13
x(5) = 9, y(5) = 21
De acuerdo con este programa, la línea de mínimos cuadrados es:
Y = 3 + 2X
Y el coeficiente de correlación es r=1.0, mientras que el error estándard de la estimación es cero, lo cual como veremos posteriormente nos dice que todos los pares de datos forman parte de la línea de mínimos cuadrados. Si graficamos la línea de mínimos cuadrados y graficamos sobre ella los pares de datos (xi,yi), comprobaremos que efectivamente todos los datos están alineados directamente sobre una recta:
lo cual nos confirma que el criterio matemático que estamos utilizando para obtener la línea de los mínimos cuadrados, la definición que tenemos del índice de correlación r son correctos, y la definición que tenemos del error estándard de la estimación, son correctos.
Hasta aquí hemos considerado un "ajuste de mínimos cuadrados" relacionados con una línea que pudiéramos llamar "ideal" desde el punto de vista matemático, en donde tenemos una variable independiente (causa) que produce una influencia sobre alguna variable dependiente (efecto). Pero se puede dar el caso de que tengamos una situación en la cual los valores que tome cierta variable dependiente se deban no a uno sino a dos o más factores. En tal caso, si la dependencia individual a causa de cada uno de los factores -manteniendo los demás constantes- es una dependencia linear, podemos extender el método de los mínimos cuadrados para cubrir esta situación, tal y como lo hicimos cuando había una sola variable independiente. Esto es conocido como una regresión linear múltiple. Para dos variables X1 y X2, esta dependencia la representamos como Y=f(X1,X2). Si tenemos un conjunto de datos experimentales para una situación como esta, la grafica de los datos se tiene que llevar a cabo en tres dimensiones, y presenta un aspecto como el siguiente:
En esta gráfica, la altura de cada punto representa el valor de Y para cada cada par de valores X1 y X2. Representando los puntos sin mostrar explícitamente las "alturas" de los puntos hacia el plano horizontal Y=0, la gráfica tridimensional toma el siguiente aspecto:
El método de los mínimos cuadrados utilizado para ajustar un conjunto de datos a una recta de mínimos cuadrados también se puede extender para obtener una fórmula de mínimos cuadrados, en cuyo caso para dos variables la ecuación de regresión será la siguiente:
Y = A0 + A1X1 + A2X2
Erróneamente y frecuentemente, esta ecuación es tomada como representando una línea. Sin embargo, no es una línea, es una superficie. Si llevamos a cabo un ajuste de mínimos cuadrados sobre esta fórmula linear con dos factores X1 y X2, obtenemos lo que se conoce como una superficie de regresión, que en este caso es una superficie plana:
Para los datos mostrados arriba, esta superficie de regresión tiene un aspecto como el que se muestra a continuación:
Si queremos obtener las ecuaciones para este plano de mínimos cuadrados, procedemos exactamente de la misma manera como lo hicimos para obtener las fórmulas con las cuales evaluamos los parámetros para obtener la recta de mínimos cuadrados; esto es, definimos las distancias verticales de cada uno de los pares ordenados de puntos hacia este plano de mínimos cuadrados:
Por extensión, los problemas que involucran más de las dos variables X y Y se tratan de una manera análoga a como lo hicimos con dos parámetros. Para obtener las ecuaciones de regresión para dos variables independientes X1 y X2, supóngase que empezamos con una relación entre las tres variables que puede ser descrita mediante la siguiente fórmula:
Y = α + ß1X1 + ß2X2
la cual es una fórmula linear en las variables Y, X1 y X2. Tenemos aquí tres parámetros independientes α, ß1 y ß2. Los valores de Y en esta línea que corresponden a X1=X11,X12,X13, ... ,X1N y X2=X21,X22,X23, ... ,X2N (usamos aquí el subscripto para distinguir cada una de las dos variables X1 y X2, y el superscripto para llevar a cabo eventualmente las sumaciones sobre los valores que hay de cada una de dichas variables) son α+ß1X11+ß2X21, α+ß1X12+ß2X22, α+ß1X13+ß2X23, ... , α+ß1X1N+ß2X2N, mientras que los valores actuales son Y1, Y2, Y3, ... ,YN respectivamente. Entonces, al igual que como lo hicimos con la ecuación de regresión en función de una sola variable, definimos las "distancias" producidas por cada trío de datos experimentales a los valores Yi de modo tal que la suma de los cuadrados de dichas distancias sea:
S = (α+ß1X11+ß2X21 - Y1)² + (α+ß1X12+ß2X22 - Y2)² + ... + (α+ß1X1N+ß2X2N - YN)²
Del cálculo, S será un mínimo cuando las derivadas parciales de S con respecto a los parámetros α, ß1 y ß2 sean iguales a cero:
Procediendo como lo hicimos cuando teníamos dos parámetros en lugar de tres, esto nos produce el siguiente conjunto de ecuaciones:
N α + ß1ΣX1 + ß2ΣX2 - ΣY = 0
αΣX1 + ß1ΣX1² + ß2ΣX1X2 - ΣX1Y = 0
αΣX2 + ß2ΣX2² + ß1ΣX1X2 - ΣX2Y = 0
αΣX1 + ß1ΣX1² + ß2ΣX1X2 - ΣX1Y = 0
αΣX2 + ß2ΣX2² + ß1ΣX1X2 - ΣX2Y = 0
Estas son las ecuaciones normales requeridas para poder obtener la regresión de Y en X1 y X2. Al efectuar los cálculos, nos resultan tres ecuaciones simultáneas de las cuales se obtienen los parámetros α, ß1 y ß2.
Existe una razón por la cual estas ecuaciones son llamadas ecuaciones normales. Si representamos al conjunto de datos correspondiente a la variable X1 como un vector X1 y al conjunto de datos correspondiente a la variable X2 como otro vector X2, considerando que estos vectores son independientes el uno del otro (usando un término del álgebra linear, linearmente independientes, lo cual significa que no son un simple múltiplo el uno del otro apuntando físicamente en la misma dirección), entonces podemos situar a dichos vectores en un plano. Por otro lado, podemos considerar a la suma de los cuadrados de las diferencias Di usadas en la derivación de las ecuaciones normales también como la magnitud de un vector Di, recordando que la longitud cuadrada de un vector es igual a la suma de los cuadrados de sus elementos (teorema de Pitágoras extendido a n dimensiones). Esto hace que el principio del "mejor ajuste" sea equivalente a buscar aquél vector diferencia Di que corresponda a la menor distancia posible hacia el plano formado por los vectores X1 y X2. Y esa menor distancia posible es un vector perpendicular o vector normal:
al plano definido por los vectores X1 y X2 (o mejor dicho, al plano formado por la combinación linear de los vectores ß1X1+ß2X2).
Aunque podemos repetir aquí las fórmulas que corresponderán al caso de dos variables X1 y X2, habiendo entendido lo que es un "plano de míminos cuadrados" podemos recurrir a uno de muchos programas computacionales disponibles comercialmente o a través de Internet. La página personal del Profesor Victor Miguel Ponce citada arriba nos ofrece los medios para poder llevar a cabo un "ajuste de mínimos cuadrados" cuando se trata del caso de de dos variables X1 y X2, accesible en la siguiente dirección:
http://ponce.sdsu.edu/onlineregression13.php
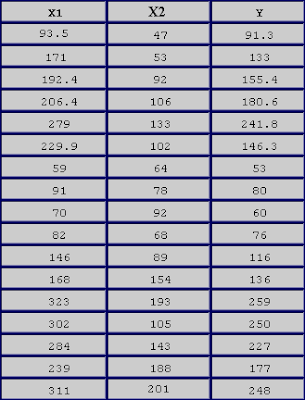
PROBLEMA: Obtener la fórmula del plano que mejor se ajusta a la representación del siguiente conjunto de datos:
Estos datos, representados en tres dimensiones, muestran el siguiente aspecto:
Para este conjunto de datos, la fórmula que corresponde a la superficie de regresión es la siguiente:
Y = α + ß1X1 + ß2X2
Y = 9.305829 + 0.787255 X1 - 0.04411 X2
A continuación tenemos un gráfico animado de la regresión linear múltiple en X1 y X2 representada por la fórmula:
Y = -2X1 + 2X2
en el cual X1 y X2 son variados desde -10 hasta +10 y la gráfica tridimensional es rotada girándola alrededor del eje Y, razón por la cual este tipo de gráficas son conocidas con el nombre de "spin plot" (es necesario ampliar la imagen para poder ver la acción animada):
El modelaje que hemos llevado a cabo se puede extender a tres variables, a cuatro variables, etc., y podemos obtener una ecuación de regresión linear múltiple:
Y = ß0 + ß1X1 + ß2X2 + ß3X3 + ß4X4 + ß5X5 + ... + ßNXN
Desafortunadamente, para más de dos variables ya no es posible hacer un graficado multi-dimensional, y en vez de confiar en nuestra intuición geométrica tenemos que confiar en nuestra intuición matemática. Después de cierta práctica, podemos abandonar nuestra dependencia en representaciones gráficas extendiendo lo que aprendimos hacia un mundo multi-dimensional aunque no nos sea posible poder visualizar lo que está ocurriendo, dando el paso crucial de generalización o abstracción que nos permite prescindir de los detalles particulares y aún así poder continuar trabajando como si nada hubiera pasado.
Una cosa importante que no hemos mencionado aún es que, para el caso de dos variables (así como más de tres variables), no hemos tomado en cuenta los posibles efectos de interacción que pueda haber entre las variables independientes. Estos efectos de interacción, que se dan con cierta frecuencia en el campo de las aplicaciones prácticas, se pueden modelar en su caso más sencillo con una fórmula como la siguiente:
Y = ß0 + ß1X1 + ß2X2 + ß12X1X2
Cuando no hay interacción alguna entre las variables , el parámetro ß12 mostrado en esta fórmula es cero. Pero si hay algún tipo de interacción, dependiendo de la magnitud del parámetro ß12 con respecto a los demás parámetros ß0, ß1 y ß2 esta interacción podría ser de tal magnitud que inclusive podría nulificar la importancia de los términos variables ß1X1 y ß2X2. Este tema por sí solo es lo suficientemente amplio como para requerir ser tratado por separado en otra sección de esta obra.