3: La parábola de mínimos cuadrados

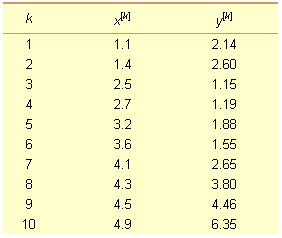
El ajuste de datos a fórmula usando un modelo linear es excelente cuando los datos sigan una tendencia linear. Sin embargo, en muchas ocasiones los datos no siguen una tendencia linear. Considérese como ejemplo la siguiente colección de diez datos:

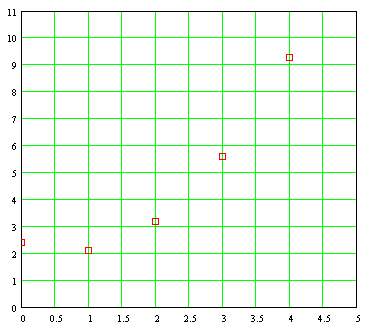
Si graficamos esta colección de diez datos, obtendremos lo siguiente:

De la gráfica no resulta claro cómo podamos describir esta colección de datos con una fórmula empírica linear. Podemos forzar una línea recta sobre esta colección de datos llevando a cabo el análisis de regresión, haciendo ciegamente los cálculos matemáticos usuales para obtener el "mejor ajuste" linear. Sin embargo, la fórmula así obtenida tal vez no nos será de mucha utilidad para estimar lo que ocurrirá con otros valores no graficados.

Si nos hacemos a la idea de que esta colección de datos puede ser mejor descrita por un modelo no-linear, entonces un primer paso hacia esta dirección consistiría en utilizar un polinomio de grado n:

Y = a + bx + cx² + dx³ + ex⁴ + ...

Lo primero que se nos podría ocurrir sería utilizar un polinomio cuyo grado corresponda directamente con la cantidad de puntos que hay en la gráfica. De este modo, así como en una gráfica en la que hay únicamente dos puntos utilizaríamos una línea recta para unir dichos puntos, en una gráfica en la que hay tres puntos usaríamos un polinomio cuadrático de grado 2, en una gráfica en la que hay cuatro puntos usaríamos un polinomio cúbico de grado 3, y así sucesivamente. Este procedimiento matemático es conocido como la interpolación. Esto ciertamente haría pasar la curva exactamente por cada uno de los puntos de la gráfica, como se muestra a continuación:

Veamos a continuación dos ejemplos de ello.


PROBLEMA: Para un experimento del cual están únicamente disponibles los tres datos que aparecen en la siguiente gráfica:

¿Cuál será la fórmula empírica que mejor se pueda ajustar a estos datos?

Intentar llevar a cabo un ajuste de mínimos cuadrados para obtener la línea de regresión que mejor se aproxime a los tres datos mostrados en la gráfica será una pérdida de tiempo, ya que los puntos no muestran tendencia alguna de agruparse en las proximidades de una línea recta. Sin embargo, podemos tratar de llevar a cabo aquí un ajuste utilizando como modelo un polinomio cuadrático, haciendo pasar los tres puntos exactamente a lo largo del polinomio:

P(X) = a₀ + a₁X + a₂X²

Sustituyendo los tres pares de datos A(X₁, Y₁)=(1,1), B(X₂, Y₂)=(2,8) y C(X₂, Y₂)=(3,2) en el polinomio cuadrático:

1 = a₀ + a₁(1) + a₂(1)²

8 = a₀ + a₁(2) + a₂(2)²

2 = a₀ + a₁(3) + a₂(3)²

obtenemos el siguiente conjunto de ecuaciones que se pueden resolver como ecuaciones simultáneas:

a₀ + a₁ + a₂ = 1

a₀ + 2a₁ +4a₂ = 8

a₀ + 3a₁ + 9a₂ = 2

De estas tres ecuaciones obtenemos como solución los siguientes coeficientes:

a₀ = -19

a₁ = 26.5

a₂ = -5.5

La fórmula cuadrática que modela exactamente los tres pares de datos es entonces:

P(X) = -19 + 26.5X - 6.5X²

La gráfica de esta fórmula cuadrática superimpuesta sobre los tres puntos discretos que la produjeron es la siguiente:

Si los datos que produjeron la fórmula cuadrática que forzada sobre dichos datos fueron recabados de la vida real, la dificultad con el método del ajuste exacto es que si se recaban posteriormente datos adicionales para valores de Y en otros puntos de X tales como X=1.5 y X=2.5, tales puntos adicionales no pueden ser utilizados para refinar el modelo, ya que su derivación no admite más que tres pares de datos; en cuyo caso la recabación de datos adicionales sólo servirá para confirmar o desechar la fórmula cuadrática obtenida, no para mejorarla y refinarla.


PROBLEMA: Llevar a cabo un ajuste exacto de los siguientes datos

X₁ = -1, Y₁ = 0

X₂ = 0, Y₂ = 0

X₃ = 1, Y₃ = 0.1
X₄ = 1.3, Y₄ = 1

a un polinomio cúbico:

P(X) = a₀ + a₁X + a₂X² + a₃X³

Hay tantos datos como coeficientes a_i en el polinomio, lo cual nos permite llevar a cabo un ajuste exacto que de otro modo no se podría llevar a cabo si hubiese menos datos que coeficientes o más datos que coeficientes. Para llevar a cabo el ajuste exacto, simplemente substituímos los pares de valores en el polinomio cúbico para obtener así cuatro ecuaciones que se pueden resolver como ecuaciones lineares simultáneas:

a₀ + a₁(-1) + a₂(-1)² + a₃(-1)³ = 0

a₀ + a₁(0) + a₂(0)² + a₃(0)³ = 0

a₀ + a₁(1) + a₂(1)² + a₃(1)³ = 0.1

a₀ + a₁(1.3) + a₂(1.3)² + a₃(1.3)³ = 1

De estas cuatro ecuaciones obtenemos los siguientes coeficientes:

a₀ = 0

a₁ = -0.898

a₂ = 0.05

a₃ = 0.948

El polinomio cúbico que representa los cuatro pares de datos es entonces:

P(X) = -.898X + 0.05X² + 0.948X³

La gráfica del polinomio cúbico superimpuesto sobre los cuatro puntos discretos que lo produjeron es la siguiente:

Todos los puntos caen exactamente sobre la curva, tal y como lo habíamos anticipado.

Una inspección de la curva nos muestra que tres de los puntos parecen estar agrupados en torno a lo que parece ser una línea casi horizontal. La única nota discordante la dá el punto situado en X₄ = 1.3, lo cual nos debe poner a reflexionar.

Si los cuatro puntos proporcionados para hacer un ajuste exacto a un polinomio cúbico hubiesen sido obtenidos experimentalmente, el hecho de que tres de los cuatro puntos parecen estar situados en torno a una línea recta nos debe hacer preguntarnos: ¿no cabe la posibilidad de que el cuarto punto no situado cerca de dicha recta haya sido el resultado de algún grave error experimental en vez de un error de naturaleza estadística? De cualquier manera, es necesario mantener la mente abierta a la posibilidad de que el punto discordante sea un dato genuino, de modo tal que si repetimos el experimento únicamente para dicho punto volveríamos a obtener un resultado cercano al que obtuvimos anteriormente. Como una alternativa para resolver esta incógnita, podemos recabar más datos experimentales obteniendo información para otros puntos que no habían sido considerados, por ejemplo X=-0.5, y X=+0.5. Pero en tal caso ya no es posible tratar de llevar a cabo un ajuste exacto a una fórmula cúbica; requeriríamos en todo caso un polinomo de quinto grado. Y si recabamos once datos experimentales, requeriríamos un polinomio de grado diez para poder llevar a cabo un ajuste exacto haciendo pasar la curva sobre todos los diez puntos. Independientemente de la complejidad matemática de estar manejando polinomios de orden creciente, está el hecho de que le estemos dando tanta importancia al hecho de forzar la curva que estamos modelando a pasar exactamente sobre todos los puntos, lo cual ignora rotundamente el hecho de que los datos experimentales siempre tienen alguna dosis de "ruido" estadístico, alguna dosis de error aleatorio que les impide caer de modo exacto sobre una curva si es que existe una curva derivada teóricamente capaz de describir lo que estamos observando. Por otro lado, la desventaja de los polinomios de alto grado es su tendencia a oscilar violentamente no solo fuera del rango de valores considerados en un experimento, sino inclusive entre las zonas intermedias a los puntos en los cuales se llevaron a cabo las mediciones. Obsérvese en la curva del polinomio de tercer grado cómo para valores inferiores a X=-1.5 el valor vertical se desploma bruscamente, ocurriendo algo similar para valores de X superiores a X=+1.5 en donde los valores de P(X) ascienden en forma aguda. Para polinomios de alto grado, este comportamiento oscilatorio violento se puede convertir en un asunto completamente impredecible, consecuencia directa de estar insistiendo en llevar a cabo un modelaje exacto que haga pasar todos los datos experimentales sobre una curva.

El procedimiento de interpolación resulta adecuado para resolver problemas analíticamente exactos, lo cual no ocurre con los datos experimentales en donde los datos rara vez "caen" exactamente en un valor que podría considerarse ideal, en donde la dispersión de los datos con respecto a un ajuste "ideal" es debida al error experimental y en donde carece de sentido el tratar de ajustar exactamente una cantidad determinada de datos a una fórmula polinómica. Es por ello que, así como en el ajuste de una fórmula linear a una colección de datos que parecen seguir una tendencia linear recurrimos al método de los mínimos cuadrados, este mismo método de los mínimos cuadrados es extendido para poder ser aplicado a fórmulas polinómicas, lo cual nos permite mantener el grado del polinomio bajo control sin permitirle que crezca desmesuradamente al ir agregando pares adicionales de puntos (en otras palabras, bajo el criterio de los mínimos cuadrados podemos tratar de ajustar 101 pares de puntos a un polinomio cuadrático o a un polinomio cúbico en vez de vernos forzados a tener que recurrir a un polinomio de grado 100 si insistimos en tratar de llevar a cabo un ajuste exacto de los datos a la fórmula que estamos desarrollando).

Si un conjunto de pares de datos al ser graficados no muestra un agrupamiento en torno a una línea recta sino en torno a una curva, como primera aproximación podemos intentar hacer un "ajuste" a la curva más elemental de todas, la parábola, lo cual en términos sencillos significa intentar llevar a cabo el ajuste de los datos a un polinomio cuadrático como el siguiente:

Y = a₀ + a₁X + a₂X²

Se ha llevado a cabo un ligero cambio de notación en los parámetros del polinomio, en preparación para la eventual generalización hacia un "ajuste" de mínimos cuadrados con una curva correspondiente a un polinomio de grado p.

Procediendo exactamente de la misma manera como lo hicimos con la recta de mínimos cuadrados, podemos postular la diferencia entre cada valor real de Y=Y₁,Y₂,Y₃,...,Y_N y cada valor calculado para su correspondiente X_i usando la ecuación cuadrática de mínimos cuadrados, lo cual nos dá la "distancia" vertical D_i que aleja a ambos valores:

D₁ = a₀ + a₁X₁ + a₂X₁² - Y₁

D₂ = a₀ + a₁X₂ + a₂X₂² - Y₂

D₃ = a₀ + a₁X₃ + a₂X₃² - Y₃

.
.
.

D_N = a₀ + a₁X_N + a₂X_N² - Y_N

Y al igual que como lo hicimos al buscar la recta de los mínimos cuadrados, también aquí extendemos el criterio de buscar el polinomio cuadrático que sea tal que la suma de los cuadrados de las distancias verticales de cada uno de los puntos "reales" a los puntos calculados de acuerdo a dicho polinomio sea un mínimo. En pocas palabras, queremos minimizar la función:

S = [a₀ + a₁X₁ + a₂X₁² - Y₁]² + [a₀ + a₁X₂ + a₂X₂² - Y₂]² + [a₀ + a₁X₃ + a₂X₃² - Y₃]

_______+ ... + [a₀ + a₁X_N + a₂X_N² - Y_N]²

Puesto que ahora tenemos tres parámetros en lugar de dos, tenemos que llevar a cabo tres diferenciaciones parciales, las cuales nos conducen eventualmente a los siguientes tres sistemas de ecuaciones:

a₀N + a₁ΣX + a₂ΣX² = ΣY

a₀ΣX + a₁ΣX² + a₂ΣX³ = ΣXY

a₀ΣX² + a₁ΣX³ + a₂ΣX³ = ΣX²Y

Este conjunto de ecuaciones es conocido como las ecuaciones normales para la parábola de mínimos cuadrados. De nueva cuenta, tenemos un sistema de ecuaciones simultáneas, con tres incógnitas, los parámetros a₀, a₁ y a₂, que definirán la curva de los mínimos cuadrados para un conjunto dado de datos que parezcan seguir un crecimiento exponencial de segundo grado.


PROBLEMA: Ajustar, según convenga, a una recta o a una parábola de mínimos cuadrados los datos dados por la siguiente tabla:

El primer paso obligado antes de tratar de ajustar una serie de datos a una fórmula consiste en poner los datos sobre una gráfica para intentar descubrir la tendencia mostrada por los datos. En este caso, la gráfica resulta ser:

Aunque a primera vista nuestro primer impulso sea el tratar de llevar a cabo un ajuste utilizando una recta de mínimos cuadrados, el punto que aparece en la gráfica para X₀=0 si realmente representa no una equivocación en la toma de una lectura sino un dato genuinamente válido nos debe llevar a pensar en la posibilidad de que los datos en vez de estar modelados por una línea recta tal vez estén modelados por una curva. Y la curva más sencilla de todas es la proporcionada por un polinomio de segundo grado, un polinomio cuadrático. Utilizando las ecuaciones normales derivadas arriba, la parábola de mínimos cuadrados resulta ser:

Y = 2.51 - 1.20X + .733X²

El graficado de esta curva, sobrepuesta sobre los datos experimentales, presenta el siguiente aspecto:

Podemos ver que el ajuste de los datos a una fórmula cuadrática es bastante bueno. Y no sólo eso, sino que nos permite detectar la presencia de lo que parece ser un mínimo. Este mínimo muy bien podría ser un punto óptimo para minimizar las pérdidas en un proceso industrial, obtener el mayor grado de pureza en un proceso químico, o lograr la mejor calidad en una aleación. Y pudimos utilizar los siete pares de datos experimentales para llevar a cabo el modelaje sin necesidad de tener que recurrir a un polinomio de grado seis si hubiéramos insistido en un ajuste exacto de los datos. Podemos ver de inmediato en la gráfica que el punto mínimo de la parábola está situado aproximadamente en el punto X=0.25, y podemos obtener una mejor aproximación numérica mediante el cálculo diferencial tomando la derivada de la parábola de los mínimos cuadrados e igualando a cero la derivada. Armados con esta información, podemos planear la conducción de un solo experimento en el cual le demos a la variable X (que se presume está bajo nuestro control) el valor 0.25 con el fin de confirmar si realmente hay allí un punto mínimo. Obsérvese el paso trascendental que estamos dando aquí. De una serie de puntos discretos, tras llevar a cabo el ajuste de los datos a una fórmula estamos anticipando la existencia de un mínimo, y no solo ello sino que estamos anticipando la zona en la cual está localizada dicho punto mínimo. Este es precisamente uno de los objetivos en ajustar una serie de datos a una fórmula, el poder utilizar dicha fórmula para intentar hacer predicciones dentro de los rangos estudiados, o inclusive extrapolar la fórmula fuera de los rangos estudiados.


PROBLEMA: Con el fin de determinar el valor de la constante g, la aceleración causada por la acción de la gravedad sobre la superficie de la Tierra, un grupo de estudiantes llevó a cabo un experimento en el cual se midió el tiempo que tardaba en caer un objeto desde un edificio a lo largo de alturas diferentes, midiéndose el tiempo a distancias prefijadas. Si los resultados obtenidos fueron los siguientes:

Considerando a t como la variable independiente y a y como la variable dependiente, ¿cuál será la parábola que mejor se ajuste a estos datos? Sabiendo que la fórmula teórica es y=½gt² en donde g es la aceleración de la gravedad, obtener el valor de g a partir de estos datos experimentales. Calcular asimismo las alturas que, según la curva de mínimos cuadrados, deberían de haber obtenido los estudiantes para cada uno de los tiempos transcurridos.

El graficado de los puntos obtenidos experimentalmente es el siguiente:

La gráfica nos indica que, dentro de los márgenes de error que se pueden esperar de cualquier experimento que se lleva a cabo, los datos parecen ajustarse mejor a una curva parabólica que a una línea recta. Utilizando las ecuaciones normales derivadas arriba, la parábola de mínimos cuadrados resulta ser:

Y = 5.089t²

La gráfica continua de esta fórmula superimpuesta sobre los datos experimentales con los que fué obtenida es la siguiente:

Si la fórmula teórica de la aceleración causada por la gravedad de la Tierra es y=½gt², entonces el valor de dicha aceleración g será:

½g = 5.089

g = 10.178

Este valor compara favorablemente con el valor conocido de g=9.8 metros/segundo². El problema demuestra que un ajuste de mínimos cuadrados se encarga de "promediar" la tendencia con respecto a los datos experimentales, y entre más datos experimentales se tengan, tanto mejor.

Este problema es representativo de aquellos problemas en los cuales se ha derivado ya previamente un modelo teórico que explica cierto comportamiento de alguna fenómeno natural, y en los cuales el propósito de llevar a cabo un ajuste de datos a una fórmula es obtener un valor para alguna constante como lo es en este caso la aceleración de la gravedad sobre la superficie terrestre.

http://www.amstat.org/publications/jse/v3n1/datasets.dickey.html


PROBLEMA: En la investigación de accidentes automovilísticos, el tiempo total requerido para el frenado total de un automóvil después de que el conductor ha percibido un peligro está compuesto de su tiempo de reacción (el tiempo que transcurre en su detección del peligro y la aplicación de los frenos) más el tiempo de frenado (el tiempo que tarda el automóvil en detenerse después de la aplicación de los frenos). La siguiente tabla proporciona la distancia de frenado D en pies de un automóvil que viaja a diversas velocidades V en millas por hora al momento en el cual el conductor detecta un peligro.

Obtener la parábola de mínimos cuadrados en la forma

D = a₀ + a₁V + a₂V²

que describe al conjunto de datos. En base a esta fórmula, estimar la distancia D de frenado cuando el automóvil se está desplazando a 45 millas por hora y a 80 millas por hora.

La parábola de mínimos cuadrados resulta ser:

D = 41.77 - 1.096V + .08786V²

La gráfica de esta fórmula superimpuesta sobre los datos dados es la siguiente:

En base a esta fórmula, las distancias de frenado cuando el automóvil se está desplazando a 45 millas por hora y a 80 millas por hora son:

D = 41.77 - 1.096(45) + .08786(45)²

D = 170 pies

D = 41.77 - 1.096(80) + .08786(80)²

D = 516 pies

Obsérvese que en este problema al hacer el cálculo de la distancia de frenado D para una velocidad V= 80 millas/hora estamos extrapolando los datos yendo más allá de la velocidad V= 70 millas/hora para la cual fueron obtenidos, haciendo una predicción que vá más allá de lo que podríamos llamar nuestra "zona de confianza". Siempre hay un riesgo al hacer este tipo de extrapolaciones, y más de un estadístico ha quedado en el ridículo al hacer este tipo de extrapolaciones, aunque en este caso el buen ajuste de los datos a una fórmula cuadrática nos debe dar cierta tranquilidad de que el resultado real no estará alejado de lo que estamos prediciendo.

Este problema es representativo de aquellos problemas en los cuales las conclusiones que se puedan sacar de los mismos pueden tener inclusive repercusiones de carácter legal.

El procedimiento que hemos estudiado en esta sección se puede extender para llevar a cabo un ajuste de un conjunto de datos a un polinomio de tercer grado, un polinomio cúbico cuya representación general es la siguiente:

Y = a₀ + a₁X + a₂X² + a₃X³

Procedemos ahora de la misma manera como lo hicimos con la parábola de mínimos cuadrados, postulando la diferencia entre cada valor real de Y=Y₁,Y₂,Y₃,...,Y_N y cada valor calculado para su correspondiente X_i usando lo que vendrá siendo la ecuación cúbica de mínimos cuadrados, lo cual nos dá la "distancia" vertical D_i que aleja a ambos valores:

D₁ = a₀ + a₁X₁ + a₂X₁² + a₃X₁³ - Y₁

D₂ = a₀ + a₁X₂ + a₂X₂² + a₃X₂³ - Y₂

D₃ = a₀ + a₁X₃ + a₂X₃² + a₃X₃³ - Y₃

.
.
.

D₁ = a₀ + a₁X_N + a₂X_N² + a₃X_N³ - Y₁

Y al igual que como lo hicimos al buscar la recta de los mínimos cuadrados, también aquí extendemos el criterio de buscar el polinomio cuadrático que sea tal que la suma de los cuadrados de las distancias verticales de cada uno de los puntos "reales" a los puntos calculados de acuerdo a dicho polinomio sea un mínimo. En pocas palabras, queremos minimizar la función:

S = [a₀ + a₁X₁ + a₂X₁² + a₃X₁³ - Y₁]² + [a₀ + a₁X₂ + a₂X₂² + a₃X₂³ - Y₂]²

+ [a₀ + a₁X₃ + a₂X₃² + a₃X₃³ - Y₃] + ... + [a₀ + a₁X_N + a₂X_N² + a₃X_N³ - Y_N]²

Ahora tenemos cuatro parámetros en lugar de tres, lo cual significa que tenemos que llevar a cabo cuatro diferenciaciones parciales con respecto a a₀, a₁, a₂ y a₃, las cuales nos conducen eventualmente a cuatro sistemas de ecuaciones simultáneas. La resolución de estas ecuaciones simultáneas procede exactamente de la misma manera que la forma en la cual se resolvieron los casos para la ecuación de regresión linear y la parábola de mínimos cuadrados, y no será repetido aquí. El resultado final de todo esto es, como ya lo deberíamos de haber sospechado, un conjunto de ecuaciones normales para el polinomio cúbico:

a₀N + a₁ΣX + a₂ΣX² + a₃ΣX³ = ΣY

a₀ΣX + a₁ΣX² + a₂ΣX³ + a₃ΣX⁴ = ΣXY

a₀ΣX² + a₁ΣX³ + a₂ΣX⁴ + a₃ΣX⁵ = ΣX²Y

a₀ΣX³ + a₁ΣX⁴ + a₂ΣX⁵ + a₃ΣX⁶ = ΣX³Y

Obsérvese que la formación de las ecuaciones normales para polinomios de grado superior va siguiendo un patrón definido, e inclusive podemos formularnos una "regla" para obtener las ecuaciones normales para un polinomio cualquiera de grado n. Sin embargo, para polinomios de grado mayor que 4, este ejercicio resulta futil por la cantidad excesiva de cálculos aritméticos repetitivos que tendríamos que estar llevando a cabo si recurrimos directamente a las ecuaciones normales tal y como están expresadas arriba, siendo esta la razón por la cual nos vemos en la necesidad de desarrollar técnicas un poco más sofisticadas que nos permitan resolver las ecuaciones normales de una manera abreviada.

Al igual que como ocurrió cuando la técnica para la obtención de la recta de mínimos cuadrados en una sola variable independiente X fue extendida para cubrir una regresión múltiple en dos o más variables X₁, X₂, X₃, etc., también la parábola de mínimos cuadrados puede ser extendida para llevar a cabo un ajuste a una fórmula con dos o más variables en términos lineares y cuadráticos. La fórmula de regresión múltiple general más sencilla posible involucrando términos lineares y cuadráticos, con sólo dos variables independientes X₁ y X₂ e ignorando la posibilidad de términos de interacción, es la siguiente:

Y = α + ß₁X₁ + ß₂X₂ + ß₁₁X₁²+ ß₂₂X₂²

Dadas las dificultades para poder visualizar las relaciones que toman lugar cuando estamos manejando o modelando fórmulas cuadráticas que involucran regresiones múltiples, el Departamento de Matemáticas y Estadística de la Universidad York en Ontario, Canadá, ha puesto a disposición de sus alumnos y de la comunidad académica mundial una página en la cual se pueden ver en forma dinámica (ya sea girando tridimensionalmente las superficies que corresponden a una regresión múltiple o variando parámetros tales como los términos de interacción) utilizando para ello archivos animados GIF generados con la ayuda del paquete computacional SAS desarrollado y vendido por la división Academic Technology Services (ATS) de la University of California at Los Angeles (UCLA). Esta página se puede descargar del siguiente domicilio:

http://www.math.yorku.ca/SCS/spida/lm/visreg.html

De esta página se ha tomado un archivo que grafica en tres dimensiones la siguiente fórmula:

Y = 20 - 2X₁ + 2X₂ - 0.2X₁² - 0.2X₂²

El archivo es el siguiente (el archivo con efectos animados se puede obtener recurriendo a la página de donde fue obtenido):

Aunque el modelaje de datos a superficies cuadráticas se puede llevar a cabo resolviendo el conjunto de ecuaciones normales producido por el modelo matemático que esté siendo considerado, los cálculos pueden resultar engorrosos y hasta fastidiosos cuando son hechos a mano a este nivel de complejidad, razón por la cual es preferible recurrir a otro método en el cual todo lo que tengamos que hacer es montar algún vector o alguna matriz de valores sobre los cuales podamos llevar a cabo los cálculos en una serie breve de pasos con la ayuda de algún programa computacional para manejar vectores y matrices. Esto es precisamente lo que veremos en la siguiente sección en donde trataremos acerca de un método matricial general que abrevia los pasos que deben llevarse a cabo para este tipo de modelajes.