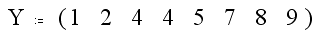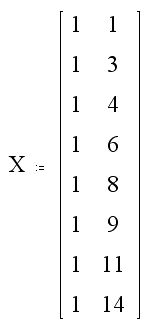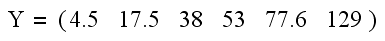4: Un método matricial general

Resulta obvio que para llevar a cabo el ajuste de datos conforme se eleva la complejidad del modelo que estamos utilizando, las sumatorias de los varios términos que es necesario llevar a cabo aunado a una creciente cantidad de ecuaciones simultáneas que hay que resolver se pueden convertir en un asunto engorrosamente burocrático.

Existe otro procedimiento más elegante que tiende a ocultar muchos de los detalles tediosos que nos distraen de nuestra labor de análisis convirtiéndola en una labor intensivamente computacional. Este procedimiento se lleva a cabo dándole a los datos numéricos una representación en forma de vectores y matrices, llevando a cabo tras esto una serie de pasos metódicos que, con la ayuda de alguno de los muchos paquetes computacionales disponibles hoy en día, nos pueden llevar con relativa rapidez a un ajuste de datos a fórmulas en un tiempo breve que en fechas recientes no hubiera sido posible.

El método que será expuesto a continuación es de naturaleza general, y supone que el lector tiene ya alguna familiaridad en el manejo de vectores y matrices y que sabe ya lo que es la inversa y la transpuesta de una matriz. (Si alguna vez algún estudiante harto de no ver una aplicación práctica inmediata a lo que estaba estudiando se llegó a preguntar hastiado para qué pueden servir las matrices, aquí tiene un buen ejemplo de ello.) Los detalles internos de la técnica serán inmediatamente obvios para quien ya ha tomado un buen curso de álgebra lineal, y no serán repetidos aquí porque lo que nos interesa es la aplicación práctica de los conceptos y no las consideraciones teóricas detrás de los mismos.

Supóngase que queremos hacer un ajuste a una recta de mínimos cuadrados:

Y = A + BX

de un conjunto de cinco pares de datos {(X_i,Y_i}. Podemos definir un vector de datos que consistirá de los cinco valores de Y acomodados como un vector renglón de valores:

Y = [Y₀ Y₁ Y₂ Y₃ Y₄ Y₅]

Hecho esto, podemos acomodar además a los cinco valores de X como una matriz de valores que tenga la siguiente forma:

Obsérvese con detenimiento que cada renglón de la matriz de datos corresponde directamente a cada uno de los puntos de datos, mientras que cada columna de la matriz corresponde directamente a cada término de la ecuación que está siendo modelada. Por lo tanto, la matriz de datos tiene cinco renglones y dos columnas. La primera columna de la matriz de datos contiene únicamente el valor de 1, puesto que ese es el valor correspondiente a los valores de los datos X cuando cada uno de ellos es elevado a la potencia cero; lo cual corresponde con el hecho de que el parámetro A en la ecuación de regresión está multiplicando a la unidad. La segunda columna de la matriz de datos contiene los valores de X, puesto que así es como aparecen los valores de X en el segundo término de la ecuación de regresión linear multiplicando al parámetro B. Si hemos de adelantarnos un poco, del mismo modo la matriz para la parábola de mínimos cuadrados tendrá tres columnas. Las primeras dos columnas serían iguales como lo fueron para el ajuste a una recta de mínimos cuadrados. Sin embargo, la tercera columna contendría el cuadrado de cada valor respectivo de X, puesto que así es como aparecen los valores de X en el tercer término de una ecuación de regresión de mínimos cuadrados para una parábola, elevados al cuadrado multiplicando un tercer parámetro C.

El siguiente paso consiste en la formación de una matriz cuadrada a partir de la matriz de datos. La matriz de datos rectangulares puede ser convertida a una matriz cuadrada, con igual número de renglones y de columnas, mediante una operación sencilla. Para ello, tomamos la transpuesta de la matriz de datos X, a la cual designaremos como X^T, y la postmultiplicamos por la misma matriz X para producir algo conocido como la matriz de coeficientes:

K = X^T ∙ X

Para una ecuación de regresión linear con cinco datos como la que hemos estado usando como ejemplo, la multiplicación de la matriz de datos X por su transpuesta X^T:

nos produce una matriz de coeficientes K que resulta ser:

Tras esto, formamos un vector designado en los libros de texto como el vector constante V:, multiplicando el vector Y por la matriz X en ese orden (recuérdese que, en la multiplicación de vectores y matrices, el orden de los factores sí altera el producto).

V = Y ∙ X

Y por último, llevamos a cabo el paso final obteniendo los parámetros deseados a través del vector solución definido como:

S = K^-1 ∙ V^T

Este vector contendrá una sola columna con varios renglones, y si se ha seguido un orden metódico entonces el primer parámetro A se podrá leer directamente del primer renglón, el segundo parámetro B se podrá leer directamente del segundo renglón, y así sucesivamente.

Es importante señalar que no hay ninguna magia en lo que hemos descrito. Los cálculos aritméticos que tienen que llevarse a cabo siguen siendo los mismos de antes. Lo que hemos hecho es ocultar los detalles, dejándole al paquete computacional que estaremos utilizando la carga de llevar a cabo las sumaciones. La necesidad de tener que resolver ecuaciones simultáneas sigue allí, está disfrazada en el paso en el cual obtenemos la inversa de la matriz de coeficientes K.

A continuación, resolveremos nuevamente el primer problema presentado en una sección anterior en el cual se llevó a cabo un ajuste de datos a una fórmula de regresión linear de Y en X usando las ecuaciones normales, esto con el objeto de que se vaya aclarando aquí la mecánica de los pasos que serán seguidos con el método matricial.


PROBLEMA: Dado el siguiente conjunto de datos

obtener la línea de regresión de Y en X usando el método matricial.

Formamos primero un vector renglón con los valores de la variable independiente Y, el cual podemos considerar como una matriz de un renglón y ocho columnas:

A continuación formamos la matriz de datos X. Puesto que el ajuste que queremos hacer es a la fórmula

Y = A + BX

entonces en base a lo que tenemos del lado derecho de la ecuación la matriz de datos X será una matriz de dos columnas (y ocho renglones) con unos en la primera columna representativos de los valores de X elevados a una potencia cero resultando en uno en todos los casos, y los ocho valores de X puestos en la segunda columna:

La matriz de coeficientes K está dada por:

mientras que el vector constante V es:

Y, por último, el vector solución S es:

De este modo, la ecuación de regresión de Y en X obtenida mediante el método matricial es:

Y = .545 + .636X

Este es el mismo resultado que el que se obtuvo anteriormente cuando se utilizaron las ecuaciones normales.

El método matricial se puede generalizar con un alcance mucho más potente en el cual radica el verdadero valor de la técnica. Tómese el caso de una ecuación no-linear como la siguiente:

en donde A, B y C son los parámetros a ser determinados para llevar a cabo el "ajuste". Podemos aplicar el método matricial a este caso de la siguiente manera: la primera columna de la matriz de datos X contendrá el simple valor numérico de 1 por las mismas razones expuestas en el problema que acabamos de ver, la segunda columna contendrá los valores recíprocos de los datos correspondientes de t, y la tercera columna contendrá el logaritmo natural de los datos. Por su parte, el vector renglón contendrá los datos correspondientes al logaritmo de ρ. Tras esto, se aplican los mismos pasos ya descritos. Cabe señalar que aquí tampoco hay ninguna magia. En realidad, lo que se está haciendo en lo que se ha señalado para esta última fórmula es llevar a cabo la linearización de la fórmula.


PROBLEMA: Obtener la ecuación de la recta "mejor ajustada" para los siguientes datos usando la técnica matricial de los mínimos cuadrados:

Montamos primero con los nueve valores de Y el vector renglón de valores, el cual es en realidad una matriz 1x9:

Y = [8.36 11.35 16.98 24.54 22.23 32.19 34.22 38.72 42.21]

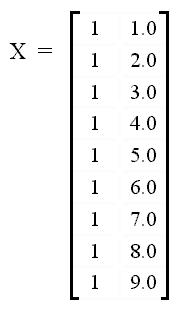
y a continuación, montamos la matriz de datos:

Tras esto, con la ayuda de algún paquete computacional para el manejo de matrices, formamos la matriz de coeficientes:

K = X^T ∙ X

y el vector constante:

V = Y ∙ X

Esto nos produce directamente el vector solución a través de la siguiente operación:

S = K^-1 ∙ V^T

que resulta ser:

El valor superior es el parámetro A de la recta de mínimos cuadrados, que viene siendo la intersección de la recta con el eje Y, mientras que el valor inferior es B, la pendiente de la recta. La ecuación deseada es por lo tanto:

Y = 4.008 + 4.327X

La gráfica de esta línea de regresión superimpuesta sobre los datos discretos a partir de los cuales fue derivada se muestra a continuación:

PROBLEMA: Obtener las ecuaciones de:

a) La parábola "mejor ajustada"

b) El polinomio cúbico "mejor ajustado"

a los siguientes datos:

a) En el primer caso, buscamos los coeficientes A, B y C para la ecuación de mínimos cuadrados:

Y = A + BX + CX²

Montamos primero con los nueve valores de Y el vector renglón de valores:

Y = [2.07 8.60 14.42 15.80 18.92 17.96 12.98 6.45 0.27]

y a continuación, montamos la matriz de datos para el ajuste a un polinomio cuadrático:

Al igual que como lo hicimos con el problema anterior, con la ayuda de algún paquete computacional para el manejo de matrices formamos la matriz de coeficientes:

K = X^T ∙ X

y el vector constante:

V = Y ∙ X

con lo cual se nos produce directamente el vector solución a través de la operación:

S = K^-1 ∙ V^T

dándonos:

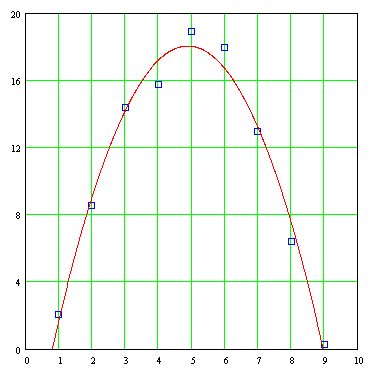
En este vector solución, el valor superior es el coeficiente A, el valor intermedio es el coeficiente B, y el valor inferior es el coeficiente C. En base a esto, la ecuación de la parábola "mejor ajustada" para los datos dados es:

Y = -7.827 + 10.59X - 1.083X²

A continuación tenemos la gráfica de esta parábola trazada junto con los datos discretos con los cuales fue generada:

Para efectuar el "mejor ajuste" a un polinomio cúbico, todo lo que tenemos que hacer es modificar la matriz X agregándole una columna adicional en el extremo derecho, llenando dicha columna con los cubos de los valores de X que están en la segunda columna:

Repitiendo exactamente los mismos pasos anteriores, obtenemos el siguiente vector solución:

Los valores en orden del vector solución son los coeficientes A, B, C y D del polinomio cúbico de mínimos cuadrados:

Y = A + BX + CX² + DX³

por lo cual el polinomio cúbico "mejor ajustado" es:

Y = -7.223 +10.012X -0.946X² - 0.009X³

A continuación tenemos la gráfica de este polinomio cúbico junto con los datos discretos a partir de los cuales se generó la fórmula:

Podemos ver que, dentro del rango de interés (desde X=0 hasta X=10), el término cúbico introdujo una corrección muy pequeña, casi insignificante, a la parábola trazada por el término cuadrático, y es dudoso que en este caso el recurrir a un polinomio de grado mayor nos produzca un ajuste "perfecto".

PROBLEMA: Resolver nuevamente, esta vez con la ayuda del método matricial, un problema previo en el cual se llevó a cabo un ajuste de datos experimentales a una parábola de mínimos cuadrados con el fin de obtener un valor aproximado de la gravedad de la Tierra. Los datos, repetidos aquí, son los siguientes:

El ajuste que queremos llevar a cabo es en este caso un ajuste de los datos a una fórmula del tipo:

Y = AX²

Como primer paso, formamos el vector Y de datos:

Como siguiente paso, formamos la matriz de datos X. En este caso, como lo podemos intuír del único término que aparece del lado derecho de la fórmula que estamos utilizando como modelo, la matriz de datos consistirá de una sola columna, la cual estará formada por los cuadrados de los valores de X:

La evaluación de la matriz de coeficientes nos produce en este caso un solo valor, puesto en una matriz de un renglón y una columna:

K = X^T ∙ X

K = [ 1032]

El vector constante también resulta ser en este caso un solo valor numérico:

V = Y ∙ X

V = [5254]

De este modo el vector solución S, el cual nos dá el valor del parámetro A como única solución, es:

S = [5.089]

Con esto, la parábola mejor ajustada de acuerdo al método matricial es:

Y = 5.089X²

Este es el mismo resultado obtenido anteriormente.