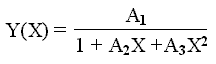6: Modelaje con funciones racionales

Una de las técnicas más versátiles para modelar un conjunto de datos a una fórmula es empleando una fórmula tal que esta sea el cociente de dos polinomios:

Una fórmula así obtenida es conocida como una fórmula racional.

Una fórmula racional es básicamente una fórmula no-linear. Para poder modelar un conjunto de datos a una fórmula racional,la estrategia consiste en "quitarle" lo racional, multiplicando ambos miembros de la fórmula que está siendo utilizada como modelo por el denominador Q(X), con lo cual nos queda una relación de la forma:

Y(X)∙Q(X) = P(X)

A continuación, quitamos los paréntesis de lado izquierdo de esta relación multiplicando todos los términos de Y(X) por todos los términos de Q(X), tras lo cual despejamos del lado izquierdo para dejar a la variable Y sola en dicho lado poniendo el resto del lado derecho. Una vez que hemos llevado esto a cabo, tenemos la fórmula justo en la forma requerida para poder aplicar el método matricial, evitándonos con ello la penosa labor de tener que estar derivando las ecuaciones normales que correspondan a cada modelo en particular que queramos utilizar.

Una cosa muy importante que siempre hay que tener en mente al llevar a cabo un modelaje utilizando una fórmula racional es buscar la presencia de raíces en el polinomio Q(X) que puedan estar dentro del rango de datos que están siendo modelados, porque tales raíces hacen que el polinomio Q(X) tome un valor de cero, trayendo como consecuencia una división por cero con la cual el valor de Y(X) toma un valor indefinido precisamente en dicho(s) punto(s). La presencia de una división por cero puede ser razón más que suficiente para desechar cierto modelo racional reemplazándolo por otro.

La expresión general para la fórmula racional utilizada para modelar datos obtenidos experimentalmente es la siguiente:

Aquí X es la variable dependiente, Y es la variable independiente, y A₁, A₂, A₃, etc. son los coeficientes a ser determinados, los cuales suponemos lineares.

Aunque la función racional es no-linear, y aparentemente fuera del alcance del método de los mínimos cuadrados, esta función puede ser linearizada despejando el denominador del lado derecho y poniéndola como:

Y(1 + A₂X + A₄X² + A₆X³ + ...) = A₁ + A₃X + A₅X² + ...

Esto puede ser reacomodado de la siguiente manera:

Y = A₁ - A₂XY + A₃X - A₄X²Y + A₅X² - A₆X³Y + ...

Algunos de los términos del lado derecho contienen tanto a la variable dependiente Y como a la variable independiente X, lo cual aparentemente constituiría un problema. Sin embargo, no lo es, porque al llevar a cabo el ajuste de datos a la fórmula tanto X como Y son vectores de valores numéricos conocidos, los mismos datos con los que se va a obtener la fórmula, y lo que nos importa a fin de cuentas son los coeficientes A₁, A₂, A₃, etc. que estamos buscando, y como todos estos coeficientes son lineares, podemos determinarlos inclusive con el método matricial que hemos estudiado.

Tal vez la fórmula racional más sencilla de todas sea la siguiente:

Y es sobre esta fórmula como llevaremos a cabo la resolución del siguiente


PROBLEMA: Ajustar el siguiente conjunto de datos

___(X₀,Y₀)=(0,2.7)____(X₁,Y₁)=(1,1.4)_ __(X₂,Y₂)=(2,0.98)_ __(X₃,Y₃)=(3,0.82)

___(X₄,Y₄)=(4,0.61)___(X₅,Y₅)=(5,0.58)___(X₆,Y₆)=(6,0.53)__ _(X₇,Y₇)=(7,0.44)

___(X₈,Y₈)=(8,0.35)___(X₉,Y₉)=(9,0.33)___(X₁₀,Y₁₀)=(10,0.33)

a una fórmula racional del tipo Y(X)=A/(1+BX).

Multiplicando ambos lados de la fórmula por 1+BX tenemos:

Y(1 + BX) = A

Despejando para poner todo en función de Y:

Y = A - BXY

Recurriendo al método matricial, construímos primero un vector Y con los datos correspondientes a Y:

Y = [2.7 _1.4_ .98_ .82_ .61_ .58_ .53_ .44_ .35_ .33_ .33]

A continuación, construímos la matriz de datos X que constará de 11 renglones y diez columnas, basándonos en la última fórmula que tenemos arriba. La primera columna contendrá únicamente "unos" (1), lo cual corresponde a los valores del parámetro X elevados a la potencia cero. Y la segunda columna estará formada por el negativo del producto de los valores respectivos de X y de Y:

Obtenemos ahora la matriz de coeficientes K:

K = X^T ∙ X

El vector constante es:

V = Y∙X

V = [9.07_ -15.158]

Por último, la solución estará dada por:

S = K^-1∙V^T

El valor que aparece en el primer renglón es A=2.506, mientras que el valor que aparece en el segundo renglón es B=0.698. Entonces la fórmula que estamos buscando es la siguiente:

La gráfica de esta fórmula superimpuesta sobre los datos discretos que la generaron es la siguiente:

Como podemos ver, el ajuste de los datos a la fórmula racional es razonablemente bueno. Podemos suponer que la razón por la cual los datos no caen exactamente a lo largo de la curva es debido al error experimental inherente a los datos por razones que están fuera del control del experimentador.


PROBLEMA: Dados los siguientes datos:

Representar estos datos con funciones racionales de "ajuste de mínimos cuadrados" usando los siguientes cocientes de dos polinomios:

(1)

(2)

(1) Aunque esta función racional es una función no-linear, podemos linearizarla multiplicando ambos miembros de la ecuación por el polinomio denominador:

Y(1 + A₂X) = A₁

Tras esto, despejamos para dejar la variable Y sola en el lado izquierdo:

Y = A₁ - A₂XY

Puesto que los coeficientes A₁ y A₂ que estamos buscando son lineares (constantes numéricas), no hay ningún problema en extender el método matricial de "ajuste de mínimos cuadrados" para obtener los coeficientes.

Formamos primero un vector Y con los valores de Y:

A continuación, formamos la matriz de datos X, observando cuidadosamente que cada columna corresponda con lo que tenemos puesto en la ecuación despejada de Y. Puesto que hay cuatro pares de datos experimentales, sabemos que esta será una matriz de cuatro renglones, y será una matriz de dos columnas correspondiendo con los términos que aparecen en el lado derecho de la ecuación despejada para Y. Al igual que en los casos anteriores que hemos estudiado en la aplicación del método matricial, la primera columna de la matriz constará de cuatro renglones con "unos". La segunda columna de esta matriz de datos, de acuerdo con lo que tenemos en el segundo término de la ecuación despejada de Y, debe estar formada por el negativo de los productos respectivos de los valores de X y de Y:

Hecho esto, aplicamos la fórmula abreviada para obtener la matriz solución con los coeficientes que estamos buscando:

S = (X^T ∙ X)^-1 ∙ (X^T ∙ Y)

Con lo cual obtenemos los coeficientes A₁=0.586561 y A₂=-0.989717. Ya con los valores de los coeficientes determinados numéricamente, la fórmula racional de mínimos cuadrados es la siguiente:

A continuación tenemos la gráfica de la curva modelada por la función racional de mínimos cuadrados con los datos discretos originales superimpuestos sobre la misma gráfica:

Resulta instructivo comparar numéricamente los valores predichos por la fórmula obtenida con los datos discretos originales:

Y(.75) = 2.27

Y(.9) = 5.368

Y(.95) = 9.81

Y(.99) = 29.06

Vemos que en los cuatro casos hay pequeñas diferencias difíciles de detectar en la gráfica.

(2) Ahora haremos el modelaje con la fórmula que aumenta un término de X² en el denominador de la función racional.

De nueva cuenta, aunque esta función racional es una función no-linear también podemos linearizarla multiplicando ambos miembros de la ecuación por el polinomio denominador:

Y(1 + A₂X + A₂X²) = A₁

Tras esto, despejamos para dejar la variable Y sola en el lado izquierdo:

Y = A₁ - A₂XY - A₃X²Y

Puesto que los coeficientes A₁, A₂ y A₃ que estamos buscando son lineares (constantes numéricas), no hay ningún problema en extender el método matricial de "ajuste de mínimos cuadrados" para obtener estos coeficientes. El vector de valores Y permanece igual, no habrá cambio alguno allí. Lo que cambiará es la matriz de datos, lo cual logramos observando cuidadosamente que cada columna corresponda con lo que tenemos puesto en la ecuación despejada de Y. Sigue habiendo cuatro pares de datos experimentales, con lo cual la matriz de datos seguirá siendo de cuatro renglones, pero ahora será una matriz de tres columnas correspondiendo con los términos que aparecen en el lado derecho de la ecuación despejada para Y. Al igual que en los casos anteriores que hemos estudiado en la aplicación del método matricial, la primera columna de la matriz constará de cuatro renglones con "unos". La segunda columna de esta matriz de datos, de acuerdo con lo que tenemos en el segundo término de la ecuación despejada de Y, debe estar formada por el negativo de los productos respectivos de los valores de X y de Y. Y la tercera columna de la matriz de datos, de acuerdo con lo que tenemos en el tercer término de la ecuación despejada de Y, debe ser formada con el negativo del producto del cuadrado de los valores de X y los valores correspondientes de Y. La matriz de datos X que nos resulta es la siguiente:

Con esto, tenemos todo lo que necesitamos para aplicar nuevamente la fórmula abreviada general para obtener la matriz solución con los coeficientes que estamos buscando:

S = (X^T ∙ X)^-1 ∙ (X^T ∙ Y)

Tras llevarse a cabo este cálculo matricial, obtenemos los coeficientes A₁=0.826773, A₂=-0.493931 y A₃=-0.492576. Con los valores de los coeficientes determinados numéricamente, la fórmula racional de mínimos cuadrados que nos resulta es la siguiente:

A continuación tenemos la gráfica de la curva modelada por la función racional de mínimos cuadrados con los datos discretos originales superimpuestos sobre la misma gráfica::

Los valores predichos por la fórmula obtenida con los datos discretos originales son los siguientes:

Y(.75) = 2.34

Y(.9) = 5.26

Y(.95) = 9.53

Y(.99) = 28.7

PROBLEMA: Dados los siguientes datos obtenidos experimentalmente:

Representar estos datos con una función racional de "ajuste de mínimos cuadrados" usando el siguiente cociente de dos polinomios:

Multiplicando ambos miembros de la ecuación por el polinomio denominador obtenemos:

Y(1 + A₂X + A₄X²) = A₁ + A₃X

Despejando para la variable Y sola:

Y = A₁ - A₂XY + A₃X - A₄X²Y

Puesto que los coeficientes A₁, A₂, A₃ y A₄ que estamos buscando son lineares, tampoco hay aquí ningún problema en extender el método matricial de "ajuste de mínimos cuadrados" para obtener los coeficientes.

Formamos primero un vector Y con los valores de Y:

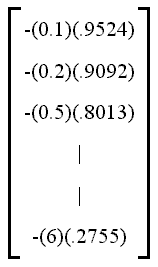
A continuación, formamos la matriz de datos X, observando cuidadosamente que cada columna corresponda con lo que tenemos puesto en la ecuación despejada de Y. Puesto que hay diez pares de datos experimentales, sabemos que esta será una matriz de diez renglones, y será una matriz de cuatro columnas correspondiendo con los términos que aparecen en el lado derecho de la ecuación despejada para Y. Al igual que en los casos anteriores que hemos estudiado en la aplicación del método matricial, la primera columna de la matriz constará de diez renglones con "unos". La segunda columna de esta matriz de datos, de acuerdo con lo que tenemos en el segundo término de la ecuación despejada de Y, debe estar formada por el negativo de los productos respectivos de los valores de X y de Y:

La tercera columna de la matriz de datos debe llevar en su tercera columna los valores de X, de acuerdo con lo que tenemos en el tercer término de la ecuación despejada de Y.

Por último, la cuarta columna, de acuerdo con el cuarto término que tenemos en la ecuación despejada de Y, debe formarse con el negativo de los productos respectivos del cuadrado de los valores de X y de los valores de Y.

Hecho esto, aplicamos la fórmula abreviada para obtener la matriz solución con los coeficientes que estamos procurando:

S = (X^T ∙ X)^-1 ∙ (X^T ∙ Y)

Con lo cual obtenemos:

Ya con los valores de los coeficientes determinados numéricamente, la fórmula racional de mínimos cuadrados es la siguiente:

A continuación tenemos la gráfica de la curva modelada por la función racional de mínimos cuadrados:

Como puede verse, el ajuste de la curva a los datos es excelente, casi ideal.

La gráfica nos ilustra otro tipo de situaciones en las cuales se utiliza una función racional para llevar a cabo el modelaje, aquellas en las cuales los datos van disminuyendo siguiendo no una línea recta sino una curva continua.


PROBLEMA: Dados los siguientes datos:

Representar estos datos con una función racional de "ajuste de mínimos cuadrados" usando el siguiente cociente de dos polinomios:

Asimismo, hacer una gráfica de la curva resultante. ¿Qué lecciones podemos aprender de este ejercicio?

Procediendo tal y como lo hemos hecho en todos los problemas anteriores, encontramos que la fórmula de mínimos cuadrados para la función racional dada es la siguiente:

Los valores predichos por esta fórmula usando los datos discretos originales son los siguientes:

Y(.75) = 2.36

Y(.9) = 5.39

Y(.95) = 9.28

Y(.99) = 29.46

De acuerdo con esto, el ajuste de los datos que tenemos es casi perfecto; todos los cuatro puntos discretos caen directamente a lo largo de la curva.

Sin embargo, al graficar la función racional obtenida, encontramos lo siguiente:

Nuestro modelo exhibe una discontinuidad severa, y de hecho tenemos dos curvas distintas. Si hacemos una prueba estadística de correlación entre los datos discretos originales y los resultados predichos por la fórmula racional en la cercanía de tales puntos, matemáticamente hablando el ajuste es casi perfecto. Sin embargo, la presencia de la discontinuidad, la cual no se puede inferir de un ajuste casi perfecto señalado por el índice de correlación, nos subraya la enorme importancia de hacer cuanto antes una gráfica de cualquier fórmula que está modelando a un conjunto de datos, porque nos podemos llevar sorpresas desagradables como esta que nos pueden obligar a desechar por completo cierto modelo. No es difícil ver el origen de la discontinuidad, ya que el polinomio cuadrático utilizado en el denominador tiene dos raíces, una de las cuales cae precisamente dentro del rango de valores que está siendo modelado, y al tomar X el valor de esta raíz se nos presenta el salto brusco que experimenta la gráfica en dicho punto.

Si repasamos los datos discretos que estamos modelando, vemos que estos datos son los mismos que utilizamos en el segundo problema de esta sección, en donde utilizamos otros modelos en cuyas gráficas no apareció el problema que tenemos aquí, ello pese a que agregamos un término adicional en el numerador (A₃X) que tal vez podría habenos dado una curva más precisa todavía. Pero esta búsqueda de precisión adicional resultó contraproducente, ya que en vez de tener una curva mejor lo que logramos fue una curva con un problema serio que no tenían las curvas anteriores. Esto remarca otro punto importante: hay que tener mucha cautela al tratar de obtener un modelo cada vez más y más complejo, porque en muchos casos, como el que hemos visto aquí, una mayor complejidad no es garantía de un mejor resultado final.