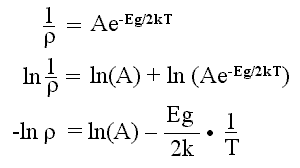El ajuste de datos experimentales a fórmulas no-lineares, al ser obvio que los datos no podrán ser ajustados ni a una recta de mínimos cuadrados ni a un polinomio de grado superior, generalmente requiere de algún modelo matemático no-linear que posea ciertas características que tal vez hasta puedan ser anticipadas teóricamente. Tómese por ejemplo el siguiente conjunto de datos experimentales:
La densidad de los datos parece agruparlos en torno a algo parecido a una curva logarítmica de la forma y=a+ln(x), de la cual podemos mostrar los siguientes ejemplos para a=0:
La obtención de las ecuaciones normales para llevar a cabo el modelaje con ecuaciones no-polinomiales se trata de manera similar al caso polinomial. La ecuación general de tres términos es:
Y = A + Bf(X) + Cg(X)
en donde f(X) y g(X) son funciones cualesquiera de la variable X. Al igual que como se hizo desde que obtuvimos las ecuaciones normales para la recta de mínimos cuadrados, definimos las distancias (residuales) como:
d = A + Bf(X) + Cg(X) - Y
Elevando los residuales al cuadrado y sumándolos, tomando tras esto las derivadas parciales con respecto a los tres parámetros A, B y C, obtenemos las ecuaciones normales:
AN + BΣf(X) + CΣg(X) = ΣY
AΣf(X) + BΣ[f(x)]² + CΣf(x) g(x) = Σf(X)Y
AΣg(X) + BΣf(x) g(X) + CΣ[g(X)]² = Σg(X)Y
AΣf(X) + BΣ[f(x)]² + CΣf(x) g(x) = Σf(X)Y
AΣg(X) + BΣf(x) g(X) + CΣ[g(X)]² = Σg(X)Y
Esta es la justificación para la extensión del método matricial general para cualquier tipo de ecuación que pueda ser linearizada.
La forma más inmediata de poder extender la cobertura del método de los mínimos cuadrados para poder utilizar modelos matemáticos no-lineares para poder ajustar datos experimentales a fórmulas no-lineares es linearizar la fórmula, lo cual muchas veces se puede llevar a cabo con procedimientos matemáticos elementales. A manera de ejemplo, la siguiente fórmula no-linear:
y = Ae-Bx
se puede linearizar tomando logaritmos naturales de ambos lados, con lo cual obtenemos:
ln(y) = ln(Ae-Bx) ln(y) = ln(A) + ln(e-Bx) ln(y) = ln(A) - Bx
lo cual graficado sobre papel logarítmico nos dá una línea recta.
Sin entrar en demasiados detalles, tal vez llegará como una buena noticia para muchos el saber que el método matricial visto previamente también puede ser utilizado para llevar a cabo el ajuste de datos a fórmulas para las cuales no parecería haber una solución sencilla bajo el método de los mínimos cuadrados. Esto se podrá apreciar mejor con la solución de unos cuantos problemas que demuestran la extensión del método matricial para poder modelar datos con fórmulas no-lineares.
PROBLEMA: Experimentalmente, se ha encontrado que la capacidad calorífica del grafito depende de una manera como lo documenta la siguiente tabla de datos en la cual se proporciona la capacidad calorífica Cp (el subíndice p indica que las mediciones fueron llevadas a cabo a presión constante, o sea "al aire libre") obtenida para varios valores de la temperatura T expresada en grados absolutos (grados Kelvin):
La experiencia ha confirmado también que una fórmula a la cual se pueden ajustar muy bien estos datos experimentales es la siguiente:
Determinar los valores de las constantes A, B y C, para la fórmula proporcionada.
Usando el método matricial, podemos linearizar el problema haciendo los valores en lo que vendrá siendo la tercera columna de datos iguales a 1/T². Formamos primero el vector renglón con los valores de Cp:
Y = [2.08 2.85 3.50 4.03 4.43 4.75 4.98 5.14 5.27 5.42]
Tras esto, la matriz de datos será la siguiente:
Nuevamente, repetimos los cálculos propios del método matricial formando la matriz de coeficientes:
K = XT ∙ X
y el vector constante:
V = Y ∙ X
para obtener el vector solución:
S = K-1 ∙ VT
lo cual nos dá los coeficientes:
A = 3.37
B = 0.00191
C = -177097
B = 0.00191
C = -177097
con lo cual la "curva de mínimos cuadrados" es:
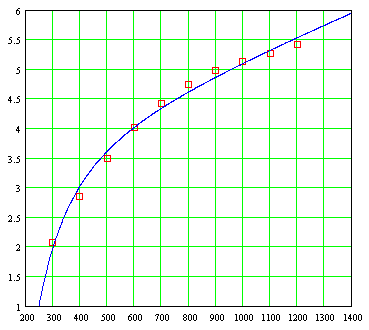
Cp = 3.37 + 0.00191T - 177097/T²
La curva, superimpuesta sobre los datos experimentales originales, es la siguiente:
PROBLEMA: La presión del vapor de agua está relacionada directamente con la temperatura. Experimentalmente se obtiene con mediciones llevadas a cabo en un laboratorio que la presión, medida en torrs, se corresponde con la temperatura, medida en grados centígrados, según los valores mostrados en la siguiente tabla:
Después de echar un vistazo a varias curvas disponibles, se encuentra que un modelo matemático que pudiera describir este comportamiento es el siguiente:
en donde la temperatura está expresada no en grados Centígrados sino en grados Kelvin (para lo cual hay que convertir grados Centígrados a Kelvin sumando 273.15) y en donde A y B son parámetros a ser estimados mediante un "ajuste de mínimos cuadrados" de acuerdo con los datos obtenidos experimentalmente en base a la tabla. Obtener A y B.
Montamos primero con los nueve valores de la presión P el vector renglón que hemos estado llamando Y (obsérvese que estamos tomando el logaritmo natural de cada valor, para corresponder con la variable que está puesta del lado izquierdo de la fórmula):
tras lo cual montamos la matriz de datos:
Formamos ahora con la ayuda de algún paquete computacional para el manejo de matrices formamos la matriz de coeficientes:
y el vector constante:
tras lo cual evaluamos el vector solución S:
obteniendo:
En este vector solución, el valor superior es el coeficiente numérico A y el valor inferior es el coeficiente numérico B. En base a esto, la ecuación "mejor ajustada" de acuerdo al criterio de los mínimos cuadrados para los datos dados es:
Una vez obtenida la fórmula, podemos graficar la curva que representa el "mejor ajuste" a los datos, superimpuesta sobre los datos discretos de los cuales fue obtenida. Aunque podemos trazar la gráfica utilizando un eje vertical logarítmico (el lado izquierdo de la ecuación), tal y como se acostumbraba en otros tiempos en los cuales la disponibilidad de programas computacionales o inclusive de tiempo de computadora compartida era un lujo casi inaccesible obligando al uso de papel logarítmico o semi-logarítmico, hoy ya no es necesario recurrir a tales artificios, y podemos "despejar" la fórmula poniendo explícitamente la presión P en función de la temperatura T, obteniendo así la siguiente ecuación y la siguiente gráfica de la fórmula con los datos discretos superimpuestos sobre la misma:
Podemos ver que el ajuste de los datos experimentales discretos a la fórmula es bastante bueno, podríamos decir casi ideal.
Esta ecuación es conocida como la ecuación de Clausius-Clapeyron. Es importante señalar que el modelo general de la ecuación fue obtenido primero teóricamente en base a argumentos basados en la termodinámica, y posteriormente el modelo fue ajustado llevando a cabo mediciones en el laboratorio con el fin de determinar los parámetros A y B con los cuales el modelo describe ya con números algo que se puede confirmar en el laboratorio.
PROBLEMA: La energía de la brecha de banda de un material semiconductor, Eg, expresada en electron-volts (eV), puede ser determinada de la siguiente fórmula:
en donde ρ es la resistividad eléctrica expresada en ohms, σ es la conductividad eléctrica expresada en mhos, k es la constante de Boltzmann que podemos tomar como 8.61x10-5, y T es la temperatura absoluta (en grados Kelvin). Los siguientes datos experimentales fueron obtenidos de un semiconductor intrínseco:
Linearizando primero la fórmula tomando los logarimos naturales en ambos lados de la misma, y llevando a cabo tras esto un "ajuste de mínimos cuadrados" sobre los datos experimentales, obtener Eg para este semiconductor.
Primero llevaremos a cabo la linearización tomando logaritmos naturales de ambos lados de la fórmula:
Al aplicar valores numéricos, esta es ya esencialmente la ecuación de una recta, en donde Eg/2kT es la pendiente de la recta.
Para este problema llevaremos a cabo algunas modificaciones que nos permitirán aligerar un poco la ejecución de los pasos que requiere el método matricial. Empezaremos con el vector renglón que normalmente escribiríamos después de tomar los logaritmos naturales de cada uno de los valores de R, escribiéndolo ahora como un vector columna:
No hay ningún inconveniente en lo que acabamos de hacer siempre y cuando tomemos la transpuesta de Y a la hora de hacer los cálculos.
A continuación, podemos definir la matriz de datos. Para ello, es importante observar que hay que convertir de grados Centígrados (o grados Celsius) a grados Kelvin (o grados absolutos) cada una de las temperaturas dadas en la tabla de valores experimentales (este es un paso necesario al resolver muchos problemas de este tipo, ya que en las fórmulas teóricas de muchos modelos científicos las referencias a temperaturas son en grados Kelvin, no grados Centígrados), para lo cual es necesario sumarle a cada temperatura el valor 273.15 en virtud de la fórmula:
Haciendo Z=273.15, la matriz de datos resulta ser:
Ahora, en vez de usar tres fórmulas matriciales diferentes como lo veníamos haciendo en los problemas anteriores, tal vez nos resulte más cómodo usar una sola. La podemos obtener del modo siguiente:
El vector renglón de datos Y lo podemos obtener tomando la transpuesta del vector columna de datos Y:
Usando ahora la propiedad de la transpuesta del producto de dos matrices:
llegamos a la fórmula condensada única:
Metiendo directamente la matriz de datos y el vector de datos (aquí es donde el investigador puede comprobar la comodidad y las ventajas de usar cierto paquete computacional científico para el manejo de matrices), obtenemos la siguiente solución en forma de un vector columna:
Entonces:
Después de echar un vistazo a varias curvas disponibles, se encuentra que un modelo matemático que pudiera describir este comportamiento es el siguiente:
en donde la temperatura está expresada no en grados Centígrados sino en grados Kelvin (para lo cual hay que convertir grados Centígrados a Kelvin sumando 273.15) y en donde A y B son parámetros a ser estimados mediante un "ajuste de mínimos cuadrados" de acuerdo con los datos obtenidos experimentalmente en base a la tabla. Obtener A y B.
Montamos primero con los nueve valores de la presión P el vector renglón que hemos estado llamando Y (obsérvese que estamos tomando el logaritmo natural de cada valor, para corresponder con la variable que está puesta del lado izquierdo de la fórmula):
Y = [ln(17.535)_ln(31.824)_ln(55.324) ... ln(760.0)]
tras lo cual montamos la matriz de datos:
Formamos ahora con la ayuda de algún paquete computacional para el manejo de matrices formamos la matriz de coeficientes:
K = XT ∙ X
y el vector constante:
V = Y ∙ X
tras lo cual evaluamos el vector solución S:
S = K-1 ∙ VT
obteniendo:
En este vector solución, el valor superior es el coeficiente numérico A y el valor inferior es el coeficiente numérico B. En base a esto, la ecuación "mejor ajustada" de acuerdo al criterio de los mínimos cuadrados para los datos dados es:
ln P = 20.459 - 5152/T
Una vez obtenida la fórmula, podemos graficar la curva que representa el "mejor ajuste" a los datos, superimpuesta sobre los datos discretos de los cuales fue obtenida. Aunque podemos trazar la gráfica utilizando un eje vertical logarítmico (el lado izquierdo de la ecuación), tal y como se acostumbraba en otros tiempos en los cuales la disponibilidad de programas computacionales o inclusive de tiempo de computadora compartida era un lujo casi inaccesible obligando al uso de papel logarítmico o semi-logarítmico, hoy ya no es necesario recurrir a tales artificios, y podemos "despejar" la fórmula poniendo explícitamente la presión P en función de la temperatura T, obteniendo así la siguiente ecuación y la siguiente gráfica de la fórmula con los datos discretos superimpuestos sobre la misma:
Podemos ver que el ajuste de los datos experimentales discretos a la fórmula es bastante bueno, podríamos decir casi ideal.
Esta ecuación es conocida como la ecuación de Clausius-Clapeyron. Es importante señalar que el modelo general de la ecuación fue obtenido primero teóricamente en base a argumentos basados en la termodinámica, y posteriormente el modelo fue ajustado llevando a cabo mediciones en el laboratorio con el fin de determinar los parámetros A y B con los cuales el modelo describe ya con números algo que se puede confirmar en el laboratorio.
PROBLEMA: La energía de la brecha de banda de un material semiconductor, Eg, expresada en electron-volts (eV), puede ser determinada de la siguiente fórmula:
1/ρ = σ = Ae-(Eg/2kT)
en donde ρ es la resistividad eléctrica expresada en ohms, σ es la conductividad eléctrica expresada en mhos, k es la constante de Boltzmann que podemos tomar como 8.61x10-5, y T es la temperatura absoluta (en grados Kelvin). Los siguientes datos experimentales fueron obtenidos de un semiconductor intrínseco:
Linearizando primero la fórmula tomando los logarimos naturales en ambos lados de la misma, y llevando a cabo tras esto un "ajuste de mínimos cuadrados" sobre los datos experimentales, obtener Eg para este semiconductor.
Primero llevaremos a cabo la linearización tomando logaritmos naturales de ambos lados de la fórmula:
Al aplicar valores numéricos, esta es ya esencialmente la ecuación de una recta, en donde Eg/2kT es la pendiente de la recta.
Para este problema llevaremos a cabo algunas modificaciones que nos permitirán aligerar un poco la ejecución de los pasos que requiere el método matricial. Empezaremos con el vector renglón que normalmente escribiríamos después de tomar los logaritmos naturales de cada uno de los valores de R, escribiéndolo ahora como un vector columna:
No hay ningún inconveniente en lo que acabamos de hacer siempre y cuando tomemos la transpuesta de Y a la hora de hacer los cálculos.
A continuación, podemos definir la matriz de datos. Para ello, es importante observar que hay que convertir de grados Centígrados (o grados Celsius) a grados Kelvin (o grados absolutos) cada una de las temperaturas dadas en la tabla de valores experimentales (este es un paso necesario al resolver muchos problemas de este tipo, ya que en las fórmulas teóricas de muchos modelos científicos las referencias a temperaturas son en grados Kelvin, no grados Centígrados), para lo cual es necesario sumarle a cada temperatura el valor 273.15 en virtud de la fórmula:
°K = °C + 273.15
Haciendo Z=273.15, la matriz de datos resulta ser:
Ahora, en vez de usar tres fórmulas matriciales diferentes como lo veníamos haciendo en los problemas anteriores, tal vez nos resulte más cómodo usar una sola. La podemos obtener del modo siguiente:
S = K-1 ∙ VT S = (XT∙X)-1) ∙ (Y∙X)T
El vector renglón de datos Y lo podemos obtener tomando la transpuesta del vector columna de datos Y:
S = (XT∙X)-1 ∙ (YT∙X)T
Usando ahora la propiedad de la transpuesta del producto de dos matrices:
(AB)T = BTAT
llegamos a la fórmula condensada única:
S = (XT ∙ X)-1 ∙ (XT ∙ Y)
Metiendo directamente la matriz de datos y el vector de datos (aquí es donde el investigador puede comprobar la comodidad y las ventajas de usar cierto paquete computacional científico para el manejo de matrices), obtenemos la siguiente solución en forma de un vector columna:
Entonces:
- Eg/2kT = -3.483 • 103
Eg = 2(8.61•105)(3.483•103)
Eg = 0.6 electron-volts
PROBLEMA: Un ejemplo notable de crecimiento exponencial lo dan las muestras de cultivos de bacterias. En la siguiente tabla, supóngase que la cantidad de bacterias por unidad de volumen está dada por la variable C después de T horas de cultivo.
Hacer un ajuste de mínimos cuadrados de los datos a una curva exponencial del tipo Y=abx. Estimar el valor de la concentración de bacterias cuando el tiempo transcurrido es de 7 horas.
Llevando a cabo los mismos pasos que los mostrados en los problemas anteriores, la curva exponencial de mínimos cuadrados resulta ser:
C = (32.14)(1.427)T
El valor de Y cuando ha transcurrido un tiempo de T=7 horas es, de acuerdo con esta fórmula:
Y = (32.14)(1.427)7
Y=387.27
Y=387.27
Obsérvese que aquí se está llevando a cabo una extrapolación, saliéndonos del rango de valores medidos para extender su alcance más allá del máximo rango cubierto por los datos que generaron la curva. Este es a fin de cuentas uno de los principales propósitos de las curvas de mínimos cuadrados: permitirle a los investigadores hacer una predicción cuantitativa que de otra manera sería muy subjetiva y propensa al error. De cualquier modo, el investigador inteligente no se limita a un solo modelo matemático, y hace lo posible por probar otros modelos en caso de que haya factores adicionales que tengan que ser tomados en cuenta para un mejor "ajuste" de datos.
La gráfica de la fórmula obtenida, superimpuesta sobre los datos experimentales discretos a partir de los cuales fue generada, es la siguiente:
Podemos ver que el ajuste de los datos a la fórmula es excelente. Existen mucho fenómenos naturales además del crecimiento de bacterias que pueden ser descritos por un modelo exponencial como el que se acaba de utilizar aquí.
Este problema es representativo de aquellos problemas que permiten hacer pronósticos con fenómenos que podrían tener que ver inclusive con la salud pública en casos de una epidemia fuera de control.
PROBLEMA: Dados los siguientes pares de datos (Xi,Yi):
(1, 5.65)
(2, 27.32)
(3, 66.7)
(4, 98.2)
(5, 159.5)
(6, 246.3)
(7, 325.7)
(2, 27.32)
(3, 66.7)
(4, 98.2)
(5, 159.5)
(6, 246.3)
(7, 325.7)
hacer un ajuste de mínimos cuadrados de los datos a una curva exponencial del tipo Y=axb.
Podemos llevar a cabo los cálculos usando el método matricial tal y como se hizo en los problemas anteriores, pero aprovecharemos la disponibilidad de una calculadora puesta a la disposición de las comunidades académicas alrededor del mundo por el Profesor Victor Miguel Ponce de la San Diego State University para llevar a cabo un ajuste de datos a una curva exponencial de mínimos cuadrados precisamente de la forma Y=axb en la siguiente dirección:
http://ponce.sdsu.edu/onlineregression12.php
Usando la calculadora, obtenemos como fórmula del "mejor ajuste":
Y = 6.104X2.056
La gráfica de los datos discretos originales superimpuesta sobre la curva exponencial generada por estos datos es la siguiente:
El ajuste parece ser un buen ajuste, con algunos puntos discretos situados ligeramente fuera de la curva.
Este problema es parecido al problema anterior excepto por una diferencia muy importante: en el problema anterior se hizo un ajuste a una fórmula de la forma Y=abX, mientras que en este problema se hizo un ajuste a una fórmula de la forma Y=aXb. Mientras que el modelo utilizado en el problema anterior intersecta al eje vertical en un punto diferente de Y=0 para X=0, el modelo utilizado en este problema intersecta al eje vertical precisamente en Y=0 para X=0, lo cual puede ser importante en algunas aplicaciones físicas en donde el crecimiento exponencial comienza precisamente a partir del "punto cero".
PROBLEMA: Después de llevarse a cabo un experimento con sumo cuidado tratando de obtener los resultados más precisos posibles, se obtuvieron los siguientes resultados:
X1 = 1, Y1 = 1.81
X2 = 2, Y2 = 0.75
X3 = 3, Y3 = 0.33
X4 = 4, Y4 = 0.146
X5 = 5, Y5 = 0.118
X6 = 6, Y6 = 0.05
X7 = 7, Y7 = 0.037
X2 = 2, Y2 = 0.75
X3 = 3, Y3 = 0.33
X4 = 4, Y4 = 0.146
X5 = 5, Y5 = 0.118
X6 = 6, Y6 = 0.05
X7 = 7, Y7 = 0.037
Ajustar estos datos experimentales a un modelo del tipo Y=aXb. ¿Qué tipo de experimento parecen estar sugiriendo los datos?
Podemos proceder tal y como lo hicimos en el problema anterior, en donde utilizamos el mismo modelo. Si hacemos esto, obtenemos la siguiente fórmula:
Y = 2.410X-2.02
La gráfica de esta curva con los datos discretos que generaron la fórmula puestos en la misma gráfica nos muestra el siguiente aspecto:
El exponente negativo de 2.02 en la fórmula parece tener un valor muy cercano al entero 2. Si suponemos que detrás de este número hay una ley natural, este número muy bien podría ser el número entero 2, lo cual tiene una repercusión inmediata, porque de acuerdo con el álgebra:
X-2 = 1/X²
El parámetro 2.410 parece ser una simple constante de proporcionalidad k para igualar las unidades en ambos lados de la fórmula, dimensionándola en forma correcta. En este caso, la fórmula se puede reescribir simbólicamente como:
Y = k ∙ (1/X²)
Nos deben quedar pocas dudas de que el experimento se trató de un experimento de algo cuyo efecto está variando en razón inversa al cuadrado de otra cantidad, una cantidad que muy bien podría ser una distancia. Es muy posible que este experimento haya sido un experimento para verificar la variación en razón inversa al cuadrado de la distancia predicha por la ley de la gravitación universal de Sir Isaac Newton, o bien un experimento para verificar la variación en razón inversa al cuadrado de la distancia de la fuerza de atracción o repulsión entre dos cargas eléctricas de signos opuestos o de signos iguales predicha por la ley de Coulomb. Se nos dice en el enunciado del problema que el experimento se llevó a cabo con sumo cuidado, y aún así varios datos experimentales discretos cayeron visiblemente fuera de la curva que efectivamente parece ser la curva de "mejor ajuste", lo cual nos dice que el experimento se llevó a cabo bajo circunstancias difíciles que requirieron toda la habilidad que los investigadores pudieron desplegar en la realización del experimento.
PROBLEMA: Un fenómeno que se dá con mucha frecuencia en la naturaleza es el fenómeno relacionado con el decaimiento exponencial (exponential decay) cuando la rapidez en la caída de cierta cantidad es directamente proporcional a la cantidad que va quedando. Para modelar un decaimiento exponencial, utilizamos una fórmula como la siguiente:
Y(X) = A·B-CX
Suponiendo, para fines de simplificación, que C=1, determinar los parámetros A y B que sean capaces de ajustar la fórmula del decaimiento exponencial al siguiente conjunto de datos:
-- tabla_valores_decaimiento_exponencial.png --
La fórmula
Y(X) = A·B-X
es una fórmula no-linear. Sin embargo, podemos linearizarla tomando logaritmos de ambos lados de la ecuación:
log[Y(X)] = log[A·B-X]
log[Y(x)] = log(A) + log[B-X]
log[Y(X)] = log(A) -Xlog(B)
log[Y(X)] = log(A) - log(B)·X
log[Y(x)] = log(A) + log[B-X]
log[Y(X)] = log(A) -Xlog(B)
log[Y(X)] = log(A) - log(B)·X
Haciendo P=log[Y(X)], Q=log(A) y R=log(B), tenemos una relación linear sobre la cual se puede aplicar un ajuste de mínimos cuadrados con la ayuda del método matricial. Montamos primero un vector de datos Y en el cual tomaremos el logaritmo de cada uno de los valores de Y:
Y = [log(35)__log(23)__log(12.1)__log(8.2) ... log(1.19)__log(0.57)]
A continuación, formamos la matriz de datos X. La primera columna deberá contener puros unos, lo cual es representativo de cada uno de los valores de X elevado a la potencia cero. Y la segunda columna deberá estar formada con el negativo de cada uno de los valores respectivos de X:
Con esto formado, podemos aplicar directamente la fórmula matricial condensada que nos dará la vector solución S:
S = (XT∙X)-1 ∙ (XT∙Y)
que resulta ser:
Es importante recordar que estos valores corresponden a la fórmula linearizada sobre la cual se tomaron los logaritmos. Los valores de A y B son obtenidos tomando el antilogaritmo de los números dados por la matriz solución, lo cual equivale a elevar la base (10) a dichos números como exponentes:
A = 101.561 = 36.392
B = 100.441 = 2.761
B = 100.441 = 2.761
La fórmula ajustada con los datos numéricos del experimento es entonces:
Y(X) = 36.392(2.761)-X
La gráfica de esta fórmula con los datos discretos que la generaron superimpuestos sobre la misma es la siguiente:
Podemos ver que la fórmula se ajusta razonablemente bien a los datos discretos con los cuales fue generada.
Si repasamos la fórmula que obtuvimos, podemos ver que el parámetro B que es igual a 2.761 es un número que está muy cercano al número e=2.7182, el cual no sólo es la base de los logaritmos naturales sino que también es un número que aparece en la solución de muchas fórmulas teóricas (exactas) que vienen de la solución de una ecuación diferencial muy sencilla:
dY/dx = -Y
Un ejemplo de esta clase de fórmulas es la del decaimiento exponencial radioactivo, el fenómeno más básico de la física nuclear. La observación de que el resultado que obtuvimos para el parámetro B está mucho muy cercano al número e nos debe hacer sospechar que en nuestro modelo el parámetro B es de hecho igual al número e. Esto nos puede llevar a refinar un poco más nuestra fórmula intentando llevar a cabo un ajuste de datos para el siguiente modelo:
Y(X) = Ae-X
En este caso, el modelaje es mucho más sencillo, ya que solo necesitamos procurar un solo parámetro en lugar de dos. Y en este caso, al llevar a cabo la linearización del modelo, podemos tomar ventaja del hecho de que el número exponenciado es el número e utilizando logaritmos naturales en lugar de logaritmos base 10, con lo cual podemos obtener un ajuste más cercano a la "realidad" predicha por un modelo teórico exacto.